How to improve assessment of balance in baseline characteristics of clinical trial participants—example from PROSEVA trial data?
Introduction
Randomization, balance and chance
Randomization in research and evidence-based medicine represents the term for random assignment of patients in one of two (or more) intervention groups. The underlying idea is that the randomization process is able to balance assignment between two (or more) groups, independent to the participant and/or investigator, and as such will avoid systematic errors in the group assignment process. However, it is recognized that groups assigned through the randomization process are not completely the same; rather the expectation is that the groups are well balanced on known and unknown (confounding) factors. Thus, after properly done randomization, only remaining imbalance should be due to chance (1,2).
The investigators are usually aware of pertinent variables prior to designing the research study. As they would want to limit the effect of potentially confounding variables, they may use different randomization strategies. Some of these techniques are block randomization, sequence randomization, balance-tool based on the most pertinent clinical variables, etc. (1). Regardless of the strategy used to improve the randomization, the resulting expense lies in the sample size requirement to enable the effective implementation of the chosen randomization strategy. Even when sample size is large, it is usually not feasible to balance on all pertinent variables through the randomization strategy. In studies with smaller targeted sample sizes it is not possible to effectively use randomization balancing strategies. Also, one needs to accept the presence of inapparent pertinent factors for which there is no effective way of balancing. What remains then are the effects of chance, which still should be considered and at times more closely evaluated.
Current state
Univariate comparisons between intervention groups
Most peer reviewed publications of clinical trials include a table with general or baseline characteristics marked as Table 1. In this table, investigators report demographic and pertinent clinical variables based on the random group assignment. This table allows readers to assess for (im) balance between groups’ characteristics, potential for selection bias, as well as applicability of the study to their practice (2). Frequently, authors report P values for the each variable in Table 1 in attempt to either support the balanced assignment in the case of non-significant P value (usually ≥0.05), or to indicate that the balance between groups was not ideal, if P value was significant (usually <0.05). The P values for each individual characteristic (variable) are calculated by univariate analysis by using Chi-Square or Fisher’s exact test, as applicable. These tests are able to measure and signify the difference among expected and observed values. However, in these cases, there is usually an oversight of the basic statistical principle of hypothesis testing. Although the investigators expect the differences to be insignificant, there is no formal preset hypothesis accompanied with the power analysis. The end result is that the Table 1 with P values as measures of “significance” frequently distracts the readers from carefully analyzing balance in presented variables. More importantly, the balance on reported variables is only assessed by the univariate method. However, pertinent demographic and clinical variables are not completely independent one from another; therefore presumed balance between groups in individual variables does not necessarily equals the overall balance between intervention groups on all pertinent clinical variables.
A different perspective
How to measure the differences in baseline characteristics between groups?
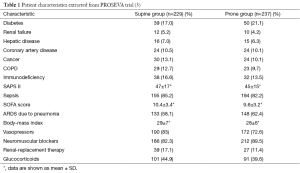
In order to better illustrate above mentioned issues, we will use the example of the recently published, “practice-changing”, PROSEVA trial (3). This was a randomized controlled trial of 16-hour prone-positioning sessions versus supine position among adults with severe acute respiratory distress syndrome (ARDS) in 26 intensive care units (ICU) in France and 1 ICU in Spain. The study showed more than 50% relative risk reduction of 28-day mortality among patients in the intervention group compared to the supine group (16% vs. 32.8%; HR =0.39; 95% CI, 0.25–0.63; P<0.001). This was reported in the accompanying New England Journal of Medicine editorial as “Virtually unprecedented in modern medicine” (4). Although our intent is not to criticize this study or explain other potential underlying reasons for the large observed mortality effect, we need to mention the fact that this study was preceded by many studies on the same topic and none of the previous ones showed significant effect on the mortality. Two meta-analyses (5,6) published since the PROSEVA trial, suggest overall benefit of probing on mortality only after the inclusion of the PROSEVA trial results. The example that we will use from this study published in New England Journal of Medicine in 2013, is the depicted as Table 1 (3).
Authors reported no significant differences between the groups in any of the baseline characteristics listed, with the exception of the Sepsis-related Organ Failure Assessment (SOFA) score, the use of vasopressors and the use of neuromuscular blockers. However, if one carefully analyzes the distribution of pertinent variables between two groups in the Table 1, it could be noted that in almost every single variable the balance is in “slight favor” of the intervention group. Diabetes as a coexisting condition was present in 21% and 17% in the prone versus supine group. Diabetes has been previously shown to be protective factor in ARDS development (7), and it was present more frequently in the prone group. There was more ARDS due to pneumonia in the prone group and it has been shown previously that the mortality of ARDS due to pneumonia (localized infection, direct ARDS) is lower than due to sepsis (systemic infection, indirect ARDS). On the contrary, there was more renal failure, hepatic disease, coronary artery disease, cancer, COPD, sepsis and immunodeficiency in the supine group, compared to the prone group. Although each of these variables individually was not deemed to be “significant”, the (not so) obvious impression is that the supine group was not only sicker than the prone group, but also with more known risk factors for ARDS. Therefore, it is suggested that there was an imbalance in baseline harmful and protective risk factors for ARDS between groups. This was in a way confirmed by significant difference in severity of illness, SOFA score, between the groups. However, another severity of illness score, SAPS II, was not deemed to be significantly different, although it was higher in the supine compared to the prone group. Moreover, the patients in supine group received significantly more vasopressors and renal replacement therapy than those in the prone group. On the contrary, they received less neuromuscular blockers, which have been recently shown to improve mortality of ARDS patients by minimizing the ventilator-induced lung injury (VILI) (8).
How did the investigators address this imbalance between groups? After acknowledging the significant between-group differences by univariate P values only in SOFA scores, the use of vasopressors and the use of neuromuscular blockers, they adjusted for these variables in the Cox proportional hazards regression model of mortality. The question is whether this was sufficient. We again emphasize here limitations of separate, univariate analyses of highly correlated variables to assess their “significance” with the outcome. Although ICU severity of illness scores were shown to be helpful in predicting mortality based on the admission variables, lumping of pertinent variables into the composite score variable and subsequent adjustment might not be ideal. This is very similar to the issue of using composite outcomes instead of the individual ones from the evidence-based medicine perspective. More importantly, the general ICU severity scores do not encompass all potentially pertinent variables as could be seen in the PROSEVA trial example, and they are not specific for ARDS or any other disease.
So, how can we then improve the assessment for imbalance in variables reported in Table 1? In order to thoroughly assess the (im) balance, all pertinent reported variables should be taken into account. There are several potential ways to address this. One way would be to include and adjust for all the variables in the multivariate model for the primary outcome regardless of the univariate P values. This method may not be practical in the trials where sample size does not allow inclusion of large number of variables (10:1 general rule). Another proposed method could be to pool the variables from Table 1 to assess their balance relative to the outcome of interest. This could be done by pooling the pertinent reported variables in a meta-analysis-like manner. However, not only the “quantity” of the difference matters. It is important to split the variables by the “quality” of their known effect on the outcome. Based on the existing knowledge and the evidence in literature, the variables should be grouped into two subgroups; one with variables with likely beneficial (protective) effect and another subgroup with variables with likely harmful effect on the outcome. For the overall pooling of both subgroups, the ordering of experimental and control groups could be reversed for easier graphical interpretation in the forest plot. Above are the forest plot examples of pooled variables from PROSEVA trial, where we used random effect model and odds ratio (OR) estimate with 95% confidence intervals (Figure 1).
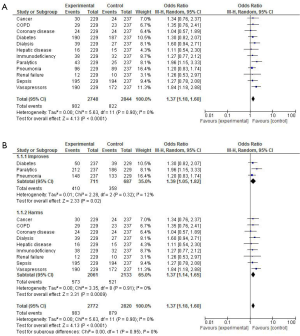
It can be seen from the forest plot examples above (Figure 1A,B) that by pooling all pertinent dichotomous variables with established direction of effect (protective or harmful) on the outcome from Table 1, one can appreciate better the difference or imbalance of the two intervention groups. The random effect model estimated the pooled difference between the groups’ baseline characteristics relative to their proposed effect towards primary outcome to be 37% higher in the control (supine) group (OR =1.37; 95% CI, 1.18–1.60; P<0.0001). Pooling of continuous variables, SAPS II and SOFA scores (Table 2), suggests that the standardized mean difference in these severity of illness scores between supine and prone groups was 0.184. Of note, the estimated effect of the SOFA score alone in the Cox proportional hazards regression model of mortality as a primary outcome in the trial was 19.4% per unit of score at inclusion (OR =1.194; 95% CI, 1.11–1.29; P<0.001). Since the observed difference in SOFA scores between two groups in Table 1 was 0.8 units (10.4 vs. 9.6), observed overall magnitude effect of SOFA score for the primary outcome was 0.155 (0.194×0.8), which is less than the observed between-the-group difference in two combined scores of severity (Table 2). More than half (~20%) of the overall proposed imbalance (37%) as estimated by the novel approach from Figure 1, remains unaccounted for by using only adjustments by severity of illness scores.

Full table
We obviously do not consider this method to be without the flaws. The main limitation is that all the variables are assumed to have similar weight on the outcome, which is certainly distant from optimal. However, despite this limitation, this method is more formal in assessing the potential imbalance between intervention groups than the current method, because it relies not only of the magnitude of the difference, but rather on the proposed direction of the effect towards outcome (quality), as well. It is novel and could be further improved to report even more accurately on balance in baseline characteristics of the intervention groups. We think that correlation and/or dependance of pertinent baseline variables can’t be ignored by choosing only the significant variables as indicated by univariate analyses. Also, by using composite estimates, as shown above with the examples of SOFA and SAPS II scores, the between-group differences could be substantially underestimated.
Other methods could prove to be more feasible, like perhaps one where the individual group’s expected and observed values from 2×2 tables for all pertinent variables can be pooled and then compared to another group by Chi-square test. However, the direction of the estimated effect on outcome of interest is of crucial importance in order to correctly estimate proper balance. We favor the first example over the second one because of easier visual interpretation with the forest plot.
Conclusions
The proposed method of assessment of potential imbalance between the intervention groups assesses not only the magnitude of the difference, but rather the pooled probability of beneficial or harmful effect towards outcome, as well. As such, it could be useful as a secondary measure for the assessment of imbalance in the trials with the unexpectedly large observed effects.
Acknowledgements
None.
Footnote
Conflicts of Interest: Abstract was presented at the American Thoracic Society conference in Denver, CO in May, 2015. No financial or other conflicts of interest are present for any of the authors.
References
- Schulz KF, Grimes DA. Generation of allocation sequences in randomised trials: chance, not choice. Lancet 2002;359:515-9. [PubMed]
- Pocock SJ, Assmann SE, Enos LE, et al. Subgroup analysis, covariate adjustment and baseline comparisons in clinical trial reporting: current practice and problems. Stat Med 2002;21:2917-30. [PubMed]
- Guérin C, Reignier J, Richard JC, et al. Prone positioning in severe acute respiratory distress syndrome. N Engl J Med 2013;368:2159-68. [PubMed]
- Soo Hoo GW. In prone ventilation, one good turn deserves another. N Engl J Med 2013;368:2227-8. [PubMed]
- Beitler JR, Shaefi S, Montesi SB, et al. Prone positioning reduces mortality from acute respiratory distress syndrome in the low tidal volume era: a meta-analysis. Intensive Care Med 2014;40:332-41. [PubMed]
- Lee JM, Bae W, Lee YJ, et al. The efficacy and safety of prone positional ventilation in acute respiratory distress syndrome: updated study-level meta-analysis of 11 randomized controlled trials. Crit Care Med 2014;42:1252-62. [PubMed]
- Moss M, Guidot DM, Steinberg KP, et al. Diabetic patients have a decreased incidence of acute respiratory distress syndrome. Crit Care Med 2000;28:2187-92. [PubMed]
- Papazian L, Forel JM, Gacouin A, et al. Neuromuscular blockers in early acute respiratory distress syndrome. N Engl J Med 2010;363:1107-16. [PubMed]