
Comparison of the accuracy of intraocular lens power calculation formulas for eyes after corneal refractive surgery
Introduction
Cataract surgery involves the replacement of an eye’s dysfunctional lens with an intraocular lens (IOL). The most critical aspect of the treatment, especially in eyes that have previously undergone corneal refractive surgery, is the calculation of IOL power, which constitutes a challenge for ophthalmologists. At present, laser-assisted in situ keratomileusis (LASIK) is the main type of corneal refractive surgery worldwide because it can provide efficient, predictable, and safe outcomes. In 1985, Peyman first introduced the concept of performing laser ablation under a corneal flap. In 1990, Pallikaris performed the first LASIK procedure in a rabbit model (1). With LASIK, a corneal flap is formed using a microkeratome and the corneal stroma is ablated using an excimer laser. Then the flap reattaches to the corneal surface.
IOL power calculation is not very precise even in unoperated eyes, where 20–25% of cases can have a prediction error in refraction higher than 0.5 diopters. Such a percentage is likely to increase when the cornea has been ablated by refractive surgery. There are three main causes of error in IOL power calculation: the keratometric index, the instrument, and effective lens position (ELP). Firstly, for calculating corneal power, the standard keratometric refractive index (normally, 1.3375) serves little purpose [P = (n − 1)/r] because the anterior to posterior corneal curvature ratio is modified by the laser (2-5). Secondly, the majority of currently available instruments extrapolate the central corneal curvature based on paracentral measurements; therefore, following myopic corneal ablation, a steeper measurement can be recorded for the corneal curvature than for the central curvature (3,6). Thirdly, the ELP error is erroneously predicted by third-generation theoretical formulas that derive their predictions from the corneal curvature (7-9).
At present, there are more than 30 methods by which the IOL power of eyes that have previously undergone corneal refractive surgery can be calculated (10). There were similar studies in comparison of IOL calculation methods in patients after LASIK. However, some formulas and methods were complicated and used more than 10 years ago (11,12). Few studies have compared the accuracy of the refractive results of the Barrett True-K with those of the other formulas, which has been recently used (13,14). Therefore, Shammas-PL, Haigis-L and Barrett True-K formulas were used in our study to compare the accuracy of IOL calculation. Of these methods, the Shammas-PL and Haigis-L formulas have been the most popular for some years. The Haigis-L formula, which is based on the regular Haigis formula, compensates for radius and keratometric index errors by using a correlation curve. It can avoid ELP errors because the ELP is derived from the depth of the anterior chamber rather than the corneal curvature. Several studies have shown that the Haigis-L formula results in fewer refractive errors (15-18). The Shammas-PL formula calculates IOL power using a modified corneal power and an estimate of postoperative anterior chamber depth (pACD), and has been reported good results in several studies (17-20). Recently, the new Barrett True-K formula, which originated from the Barrett Universal II formula, in which the keratometric value is modified, has been used to calculate IOL power in eyes with previous refractive surgery. The formula can be used for no charge on the Asia-Pacific Association of Cataract & Refractive Surgeons (www.apacrs.org) and the American Society of Cataract and Refractive Surgery websites. However, few studies have compared the accuracy of the refractive results of the Barrett True-K with those of the other formulas. Therefore, this study aimed to evaluate and compare the accuracy of the Haigis-L, Barrett True-K and Shammas-PL formulas for calculating IOL power in eyes that had previously undergone corneal refractive surgery. We present the following article in accordance with the STROBE reporting checklist (available at http://dx.doi.org/10.21037/atm-20-4624).
Methods
Patients
The records of consecutive patients who had received cataract surgery after undergoing earlier LASIK or photorefractive keratectomy (PRK) for myopia in Beijing Tongren Hospital, from October, 2017, to September, 2019, were retrospectively reviewed. The inclusion criteria were as follows: (I) the manifest refraction values were measured at ≥3 months after cataract surgery; (II) the patient had corrected distance visual acuity of 20/32 or better; and (III) the patient had experienced no perioperative or postoperative complications in relation to cataract surgery. The exclusion criteria were as follows: a history of other ocular surgery, corneal disease, uveitis, vitreoretinal disease, trauma, systemic disease affecting vision, intraoperative and postoperative complications during refractive or cataract surgery. All cataract surgical procedures involved a clear corneal incision being made, phacoemulsification, and foldable IOLs being implanted in the capsular bag. The partial coherence interferometer (IOLMaster, V.7.5, Carl Zeiss Meditec, Inc., Dublin, CA) was used to perform ocular biometry. The Haigis-L formula value provided by the IOLMaster informed the surgeon’s selection of the power of the IOL that was implanted. All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Institutional Review Board (IRB) of Beijing Tongren Hospital (NO.: TRECKY 2020-027). Because of the retrospective nature of the research, the informed consent is not required.
Calculation formulae
This study analyzed the accuracy of the Haigis-L, Shammas-PL, and Barrett True-K formulas. The IOL power calculated using the Haigis-L formula was determined by the IOLMaster reporter, which is available from the IOLMaster software. The Shammas-PL formula, which was recommended by Shammas and his colleagues, uses a modified corneal power and estimated pACD (20). The equation of corneal power is 1.14× Kpost-6.8, where Kpost represents the post-LASIK k-reading in diopters. The equation of pACD is (0.5835 × A)-64.40, where A represents the A-constant of the IOL being used. The Barrett True-K formula is based on the Barrett Universal II formula, and modified keratometry and Double-K solution were used. The calculation of IOL power with the Barrett True-K formula was performed using the web-based ASCRS IOL power calculator.
Refractive prediction error
The refractive prediction error was calculated from the difference between the actual postoperative refractive outcome and the predicted refraction for each formula or method. For each formula or method the mean numerical error, median absolute error, mean absolute error, and the percentages of eyes within ±0.50 diopter (D) and ±1.00 D of the target refraction were calculated.
Statistical analysis
All statistical analysis was conducted using R (version 1.2.1335). The continuous variables were expressed as mean ± standard deviation (SD), while categorical variables were expressed as frequencies and percentages. The one-sample t test was used to determine Whether or not the mean numerical refraction prediction error produced by each method was significantly different from zero was determined using a one-sample t-test. Differences in the refractive prediction error between the three methods were compared using analysis of variance. Fisher’s F-test was used to assess the consistency of the prediction performance of the three formulas by testing variances in the mean numerical refractive prediction errors. The absolute refractive prediction errors were evaluated with the Wilcoxon signed-rank test. Comparisons between the percentages of eyes within certain refractive prediction errors were made using the Chi-Squared test. The Bonferroni correction was applied for multiple tests. Each statistical test was two-sided, with a P value of <0.05 showing statistical significance.
Results
This study included 28 patients (32 eyes) who met the inclusion criteria. At the time of receiving LASIK or PRK, the average age of the patients was 33.5 years old, and at the time of receiving cataract surgery, it was 51.87 years old (Table 1). The average LogMAR corrected distance visual acuity prior to cataract surgery was 0.14 (range, 0.02 to 0.40). The power of the IOLs implanted ranged from 9.0 to 28.5 D. The average axial length was 28.70 mm (range, 23.08 to 34.62 mm).

Full table
Refractive prediction error
The average arithmetic IOL prediction error with the Haigis-L, Barrett True-K and Shammas-PL formulas, was −0.65, −0.39, and −0.46, respectively. Box plots of the refractive prediction errors of the three formulas tested are shown in Figure 1. For all three formulas, the mean numerical error was significantly different from zero (P<0.001). Table 2 shows the median absolute errors of the formulas (range, 0.40 and 0.57). The lowest median absolute error belonged to the Barrett True-K formula, which was significantly lower than that of Haigis-L formula (P<0.05) but similar to that of the Shammas-PL formula (P>0.05).
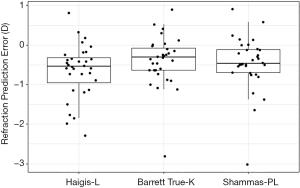

Full table
Refractive prediction error within ±0.5 and ±1.00 diopter
There was no significant difference between the percentages of eyes with a refractive prediction error within either ±0.5 D or ±1.0 D across the three formulas (Table 3).
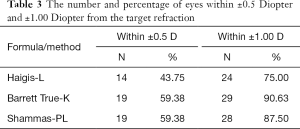
Full table
Discussion
LASIK is a routine corneal refractive surgery with high safety and few complications. Complications such as diffuse lamellar keratitis, epithelial ingrowth, flap wrinkles, free cap, dry eye and so on are rare. Many studies have proven that corneal laser refractive surgery are associated with cataractogenesis (21-23). During LASIK surgery, laser irradiation and increased suction may promote cataract development in animal studies (24,25).
Although the accuracy of IOL calculation methods after myopic laser refractive surgery has been improving, calculating IOL power is still challenging. Our study compared the accuracy of the Haigis-L, Shammas-PL, and Barrett True-K formulas for calculating the IOL power in eyes that had previously undergone myopic corneal refractive surgery. We found that the Barrett True-K formula had higher accuracy than the Haigis-L formula but performed to a similar level as the Shammas-PL formula.
In our study, the refractive prediction errors were −0.65, −0.46, and −0.39 with the Haigis-L, Shammas-PL, and Barrett True-K formulas, respectively, which is similar to the findings of Cho (26) and Vrijman (27). Compared to the results published by Abulafia, the refractive prediction errors of three formulas were −0.50, −0.34, and −0.20, respectively (17). In our study the Barrett True-K formula having a higher refractive prediction error value compared to other studies. These differences could be attributable in part to the higher degree of myopia as well as the longer mean axial length in our study, which was 28.70 mm compared with 25.69 mm in Abulafia’s study (17).
Currently, the absolute prediction error is expected to fall within ±0.5 D in 60–70% of eyes; Although there was no significant difference in the percentages of eyes with a prediction error within ±0.50 D or ±1.00 D using the three formulas in our study, the Barrett True-K formula performed much better compared to the Haigis-L formula. Similar results were published in the previous studies (17,28). In Abulafia’s study, the percentage of eyes within ±0.5 D was 46.7%, 50.0%, and 63.3%, and the percentage within ±1.00 D was 76.7%, 80.0%, and 80.0% using Haigis-L, Shammas-PL, Barrett True-K formula, respectively (17). Future studies should focus on a large number of eyes.
The results from our study showed the Barrett True-K formula to have the smallest median absolute refraction prediction error and the greatest percentage of eyes within ±0.50 D and ±1.00 D of the refractive prediction error. We speculate that the reasons for this are as follows: modified keratometry and the Double-K solution can make keratometry closer to the true keratometric power, and the Barrett Universal II formula can increase the accuracy of the IOL power calculation, although the mathematical formula behind this method has not been published. Our results show that the Barrett True-K formula can achieve the most accurate IOLs calculation.
One limitation of this study is that the three formulas used are calculation methods for eyes without historical data. There are also methods for calculating the IOL power in eyes with historical data, the accuracy of which we will compare in future research. The second limitation is the study’s retrospective design. However, all data was collected following stringent guidelines, which probably makes retrospective data more robust. The third limitation is the small sample size. A larger number of eyes should form the basis of future studies. Finally, some new methods which differ from the traditional principles, such as intraoperative aberrometry (15,29) and ray-tracing (30,31), should be applied for calculating the IOL power in eyes that have previously undergone a myopic corneal refractive operation. However, we were unable to access to the instruments required to perform those methods.
In conclusion, the Barrett True-K formula gave a superior performance to the Haigis-L formula in predicting IOL power in eyes that had previously undergone myopic corneal refractive surgery. Barrett True-K formula, as a new calculation formula, has been used since in recent years. There are few studies to compare the accuracy of IOL calculation to the other formulas. However, based on the results from our study, we think the Barrett True-K formula might become more popular among the patients after corneal refractive surgery. In future, more investigations need to be carried out so that the accuracy of the Barrett True-K formula can be evaluated with a large sample size and new methods such as ray-tracing or intraoperative aberrometry.
Acknowledgments
Funding: None.
Footnote
Reporting Checklist: The authors have completed the STROBE reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-4624
Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-4624
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-4624). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Institutional Review Board (IRB) of Beijing Tongren Hospital (NO.: TRECKY 2020-027). Because of the retrospective nature of the research, the informed consent is not required.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Pallikaris IG, Papatzanaki ME, Stathi EZ, et al. Laser in situ keratomileusis. Lasers Surg Med 1990;10:463-8. [Crossref] [PubMed]
- Gobbi PG, Carones F, Brancato R. Keratometric index, video keratography, and refractive surgery. J Cataract Refract Surg 1998;24:202-11. [Crossref] [PubMed]
- Spadea L, Iozzo N.. EBOV-RNA test with RT-PCR in ocular fluids of Ebola survivors can help to safely perform cataract surgery. Ann Transl Med 2018;6:S29. [Crossref] [PubMed]
- Mandell RB. Corneal power correction factor for photorefractive keratectomy. J Refract Corneal Surg 1994;10:125-8. [PubMed]
- Seitz B, Langenbucher A, Nguyen NX, et al. Underestimation of intraocular lens power for cataract surgery after myopic photorefractive keratectomy. Ophthalmology 1999;106:693-702. [Crossref] [PubMed]
- Chen S, Hu FR. Correlation between refractive and measured corneal power changes after myopic excimer laser photorefractive surgery. J Cataract Refract Surg 2002;28:603-10. [Crossref] [PubMed]
- Hoffer KJ. The Hoffer Q formula: a comparison of theoretic and regression formulas. J Cataract Refract Surg 1993;19:700-12. [Crossref] [PubMed]
- Holladay JT, Prager TC, Chandler TY, et al. A three-part system for refining intraocular lens power calculations. J Cataract Refract Surg 1988;14:17-24. [Crossref] [PubMed]
- Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula. J Cataract Refract Surg 1990;16:333-40. [Crossref] [PubMed]
- Savini G, Hoffer KJ. Intraocular lens power calculation in eyes with previous corneal refractive surgery. Eye Vis (Lond) 2018;5:18. [Crossref] [PubMed]
- Wang L, Booth MA, Koch DD. Comparison of intraocular lens power calculation methods in eyes that have undergone laser-assisted in-situ keratomileusis. Trans Am Ophthalmol Soc 2004;102:189-96; discussion 196-7. [PubMed]
- Hamed AM, Wang L, Misra M, et al. A comparative analysis of five methods of determining corneal refractive power in eyes that have undergone myopic laser in situ keratomileusis. Ophthalmology 2002;109:651-8. [Crossref] [PubMed]
- Savini G, Barboni P, Zanini M. Intraocular lens power calculation after myopic refractive surgery: theoretical comparison of different methods. Ophthalmology 2006;113:1271-82. [Crossref] [PubMed]
- McCarthy M, Gavanski GM, Paton KE, et al. Intraocular lens power calculations after myopic laser refractive surgery: a comparison of methods in 173 eyes. Ophthalmology 2011;118:940-4. [Crossref] [PubMed]
- Fram NR, Masket S, Wang L. Comparison of Intraoperative Aberrometry, OCT-Based IOL Formula, Haigis-L, and Masket Formulae for IOL Power Calculation after Laser Vision Correction. Ophthalmology 2015;122:1096-101. [Crossref] [PubMed]
- Haigis W. Intraocular lens calculation after refractive surgery for myopia: Haigis-L formula. J Cataract Refract Surg 2008;34:1658-63. [Crossref] [PubMed]
- Abulafia A, Hill WE, Koch DD, et al. Accuracy of the Barrett True-K formula for intraocular lens power prediction after laser in situ keratomileusis or photorefractive keratectomy for myopia. J Cataract Refract Surg 2016;42:363-9. [Crossref] [PubMed]
- Wang L, Tang M, Huang D, et al. Comparison of Newer Intraocular Lens Power Calculation Methods for Eyes after Corneal Refractive Surgery. Ophthalmology 2015;122:2443-9. [Crossref] [PubMed]
- Savini G, Barboni P, Carbonelli M, et al. Intraocular lens power calculation after myopic excimer laser surgery: Selecting the best method using available clinical data. J Cataract Refract Surg 2015;41:1880-8. [Crossref] [PubMed]
- Shammas HJ, Shammas MC. No-history method of intraocular lens power calculation for cataract surgery after myopic laser in situ keratomileusis. J Cataract Refract Surg 2007;33:31-6. [Crossref] [PubMed]
- Krueger RR, Seiler T, Gruchman T, et al. Stress wave amplitudes during laser surgery of the cornea. Ophthalmology 2001;108:1070-4. [Crossref] [PubMed]
- Mansour AM, Ghabra M. Cataractogenesis after Repeat Laser in situ Keratomileusis. Case Rep Ophthalmol 2012;3:262-5. [Crossref] [PubMed]
- Abdelkawi SA, Ghoneim DF, Atoat W, et al. 193 nm ArF excimer laser and the potential risk for cataract formation. Journal of Applied Sciences Research 2010;6:796-805.
- Costagliola C, Balestrieri P, Fioretti F, et al. Arf 193nm excimer laser corneal surgery and photo-oxidation stress in aqueous humor and lens of rabbit: one-month follow-up. Curr Eye Res 1996;15:355-61. [Crossref] [PubMed]
- Müller-Stolzenburg N, Schründer S, Helfmann J, et al. Fluorescence behavior of the cornea with 193 nm excimer laser irradiation. Fortschr Ophthalmol 1990;87:653-8. [PubMed]
- Cho K, Lim DH, Yang CM, et al. Comparison of Intraocular Lens Power Calculation Methods Following Myopic Laser Refractive Surgery: New Options Using a Rotating Scheimpflug Camera. Korean J Ophthalmol 2018;32:497-505. [Crossref] [PubMed]
- Vrijman V, Abulafia A, van der Linden JW, et al. ASCRS calculator formula accuracy in multifocal intraocular lens implantation in hyperopic corneal refractive laser surgery eyes. J Cataract Refract Surg 2019;45:582-6. [Crossref] [PubMed]
- Potvin R, Hill W. New Algorithm for Intraocular Lens Power Calculations After Myopic Laser in Situ Keratomileusis Based on Rotating Scheimpflug Camera Data. J Cataract Refract Surg 2015;41:339-47. [Crossref] [PubMed]
- Ianchulev T, Hoffer KJ, Yoo SH, et al. Intraoperative refractive biometry for predicting intraocular lens power calculation after prior myopic refractive surgery. Ophthalmology 2014;121:56-60. [Crossref] [PubMed]
- Savini G, Bedei A, Barboni P, et al. Intraocular lens power calculation by ray-tracing after myopic excimer laser surgery. Am J Ophthalmol 2014;157:150-153.e1. [Crossref] [PubMed]
- Mackool RJ, Ko W, Mackool R. Intraocular lens power calculation after laser in situ keratomileusis: Aphakic refraction technique. J Cataract Refract Surg 2006;32:435-7. [Crossref] [PubMed]


