Using a deep recurrent neural network with EEG signal to detect Parkinson’s disease
Introduction
In the brain, the maximum number of the neurons is reached at birth (1), and, unlike other cells in the human body, these neurons cannot be repaired. Thus, over the time, neurons die and fail to be replaced (2). Usually, Parkinson’s disease (PD) arises from the death of these nerve cells (3). The nerve cells generate dopamine, which is a chemical substance that mainly controls the body’s motion. Therefore, the quantity of the generated dopamine decreases when nerve cells die, which begins to affect the multiple communication modes of the brain (4). This disease appears mostly in people 50 years or older. Unstable posture, muscle stiffness, slow movement, tremor, loss of balance, and reduced fine motor skills are some initial signs of PD (4).
Statistically, about 10 million people suffer from PD (as reported by the World Health Organization) (5). If there are no visible motor (or non-motor) signs, it becomes difficult to detect PD. Hence, intelligent detection methods can be valuable for the early diagnosis of abnormal signs (6,7). As automated diagnosis systems, these methods are able to objectively detect PD by electroencephalogram (EEG) signals. Using the EEG signals, functions of cortical (or sub-cortical) segments in the brain can be easily detected. Other disease brain-related diseases, such as Alzheimer’s and epilepsy, can be identified by these signals (8-11). We thus aimed to use these EEG signals to configure a computer-aided system capable of diagnosing PD.
As is evident from the literature, EEG signals are complicated and inherently non-linear. So, most of the linear feature selection methods cannot be precisely applied to EEG signals (7). These signals of PD patients have a higher frequency band (12-15). Therefore, implementing non-linear feature extraction methods may be helpful for distinguishing between healthy and PD EEG signals.
In this way, deep neural networks, as a subsection of machine learning methods, have recently been applied to good effect in various fields of pattern identification and natural language processing (16). Deep learning methods are a subgroup of machine learning techniques known as deep network structures, with this idea being first introduced in the form of cybernetics (17). It was not immediately considered to be a practical concept due to three main limitations: the lack of an adequate dataset, the lack of computational tools to manage high-dimension networks, and a lack of effective learning methods. These limitations have been since overcome by the advent of efficient computing methods and tools.
Thus far, these methods have been successfully applied in several fields: for instance, in computer vision for Google Goggles by employing deep learning methods in object detection; in expert systems like Alpha Go, which is programmed by DeepMind (18); and for medical applications that help companies design new drugs (19).
Deep recurrent neural networks (DRNN) are very common forms of deep learning methods reported in the literature (20,21). For presenting a view of performed works in this field, proposed methods based on artificial intelligence for learning important features are provided in this section. As an example, Spadoto et al. (22) proposed the OPF classification (Optimal-Path Forest) method to diagnose the PD disease. Then, same authors suggested another method based on an evolutionary algorithm for selection of most important features to enhance the PD diagnosis precision (23). Due to parameterless and easy-application features of OPF method, it seems to be a proper method for this aim.
In the study of Soleimaniangharehchopogh et al. (24), an artificial neural network is proposed with multi-layer perceptron for diagnosis of PD impacts. Pereira et al. (25) applied sound-based properties and complex valued neural networks for helping Parkinson disease detection.
Most of performed works addressing PD computer-aided detection methods are signal-based methods (26). Nevertheless, some algorithms are also proposed based on image processing methods in the literature to diagnose PD disease. Writing tests utilizing visual trained are used in Peker et al.’s research (27) to detect the Parkinson’s disease, and they designed a dataset named ‘HandPD’ containing all extracted images/features from handwriting tests. Also, a convolutional neural network is employed for data analysis of handwritten dynamics in the context of computer-aided Parkinson’s disease detection (28).
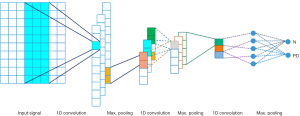
With reference to the relevant studies, we developed a novel computer-aided method to automatically detect PD by using a pooling-based deep recurrent neural network (PDRNN) model for the first time. Several RNN layers are attached into a deep configuration achieving the DPRNN neural network. A certain implementation of RNN layers is considered here (long short-term memory) to obtain the best efficiency of RNN neural network. This neural network is a novel pooling technique that can address the over-fitting problem through introduction of a new data dimension. A novel computer-aided method is developed in this study that classifies the used dataset into two Parkinson and healthy groups. Configuration of the suggested model is depicted in Figure 1. The utilized neural network is comprehensively described in the next parts.
We present the following article in accordance with the TRIPOD reporting checklist (available at http://dx.doi.org/10.21037/atm-20-5100).
Methods
Proposed deep learning method
Deep learning is a class of machine learning method, which successfully hybridizes feature extraction and clustering procedures (4,29-31). In the present work, the obtained characteristics from the considered dataset were utilized for construction of a robust DRNN model. Then, they were used for validation of the detection efficiency of the trained model in the testing stage. The efficient application of the DRNN model has been reported in the literature (20,21).
Deep recurrent network with Long Short-Term Memory (LSTM) units
Convolutional deep NNs, deep sparse autoencoders, DRNNs, and multi-layer perceptrons are some ordinary configurations of deep learning methods (32). Among these methods, DRNN was used in our study for detection of PD.
In this deep network, several RNN layers are connected to each other to structure a deep configuration (20). We used a state-of-art recurrent network as the LSTM in order to obtain the highest efficiency of the RNN network.
Here, the structure of the DRNN is presented first and followed by a description of how the LSTM units were applied to the structured DRNN.
DRNN architecture
The sharing states of this configuration are separated into several layers in order to obtain the advantages of deep structures. The higher efficiency of deep structures of recurrent is reported in various sources (20,21).
The RNN maps the input vector (x) to the equivalent output set (y). In this graph, the learning procedure is carried out in each time-step in the range of t =1 to τ. The sharing states related to the variables of each node in the lth layer are updated as follows (26):
|
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
In which, x(t) denotes the input in time-step t; y(t) and ytarget(t) are the predicted and real outputs; hl(t) indicates the sharing states of layer l; al(t) is the input of lth layer that is composed of (I) x(t) or hl−1(t), (II) b (bias values), and (III) hl(t−1). Because of the shared features of the recurrent neural network, it is able to learn the iterated uncertainties of the prior time-steps.
Applying the LSTM units
The LSTM is a certain configuration of recurrent networks that can tackle the non-solved long-term dependencies of the standard RNN configuration. In the learning process, the recurrent network aims to learn the presentation of frequently occurring patterns in the past via sharing the variables across all of the time-steps. However, the memory of the previously learned patterns can fade over the time. Dependencies of the past two input values (x(0) and x(1)) become weaker in the predicted output once it has a reasonably large value.
Consequently, long short-term memory was proposed to overcome this problem by generating paths through which the gradient is able to flow in long periods. The computing process of this unit depicts the manner of memorizing the long-term patterns by LSTM units.
Unlike conventional recurrent networks, LSTM units use a certain sharing-variables vector of S(t) (memory variable vector), which is used for storing the memorized data. The memory variable is composed of the three following operations in all time-steps:
- Elimination of the unnecessary data from S(t);
- Addition of new i(t) data chosen from x(t) and h(t−1) to the memory vector;
- Acquisition of the new h(t) from the S(t)vector.
From the depiction in the LSTM units, only two operations are conducted over h(t) including memorizing the new data and eliminating the out-of-time data. Thus, the sharing memory is able to preserve the helpful data for a sufficient time, which leads to an increase in RNN efficiency.
Suggested deep learning configuration
The structure of the developed model is outlined in Figure 1. Two phases are considered for this model: the learning and testing phases. The stratified 10-fold cross validation is presented in the training phase, in which the used dataset is divided into 10 uniform sections. From these sections, 9 are used for the training phase, and 1 one section is used in the testing phase. This process is repeated 10 times, in a way in which all 10 sections are used in both stages. In addition, for evaluating the training progression in the ending of the epochs, 20% of the learning dataset is assigned to validate the derived model. Moreover, the Single Sign On (SSO) optimizer (33) is employed, along with a few activation functions, such as Relu in all layers and softmax in the end layer. Also, dropout is adjusted to 0.5 in the dropout layer.
Results
Parkinson’s and healthy cases
The EEG signals for 20 Parkinson patients (10 males and 10 females) were collected from Henan Provincial People’s Hospital (People’s Hospital of Zhengzhou University). The ages of these patients ranged from 45 to 65, and their mean sickness period was 5.75±3.52 years (range, 2–10 years). The Hoehn and Yahr phases were in the following form (34):
- Phase 1: two patients;
- Phase 2: eleven patients;
- Phase 3: seven patients.
The obtained Mini-Mental State Examination (MMSE) results were within the range of the typical boundaries of 25 to 30 (26.9±1.51). Presence of further neurological situations or psychiatric disturbances were the exception conditions. The L-dopa drugs were used by Parkinson’s patients for decrement of non-uniformity.
Furthermore, 20 healthy cases with equal age range (9 males and 11 females) without past a record of neurological (or mental) disorders were also examined. The MMSE results obtained from the healthy cases were in the range of 27.15±1.63 years. Both the healthy and Parkinson’s cases were right-handed as determined by the Edinburgh Handedness Inventory. All patients’ had perfectly sound hearing.
All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Medical Ethics Committee of Henan Provincial People’s Hospital (2019-031) and informed consent was taken from all the patients.
Preprocessing phase and EEG signals
The required recordings were performed for 5 minutes in the steady state with a 128-Hz sample rate. For this, we used an emotive EPOC neuroheadset with 14 channels. Participants were asked sit comfortably in the appointed silent room. Then, before recording, they were instructed not to move their body in any way (including blinking) during the recording process. Afterwards, the recorded signals were divided into 2-second window lengths.
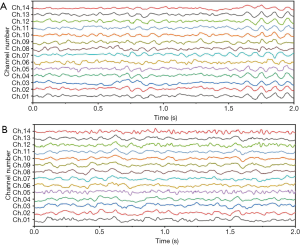
We employed a threshold method for eliminating the signals at a level higher than ±100 μV (in order to eliminate the eye-blinking effects). Subsequently, the frequencies were filtered using a Butterworth six-order band-pass filter with the forward-reverse method. This filtering was performed in order to bind the frequencies at the interval of (1) Hz. At last, 1,588 artifact-free epochs were additionally analyzed. Figure 2 shows an example of EEG signals recorded from both healthy and Parkinson’s participants.
PDRNN analysis
The suggested PDRNN model was applied over all of the EEG signals. The proposed PDRNN model was implemented in Python environment and was run in a PC with an Intel-Xeon 2.4 GHz processor and 24 GB of random-access memory.
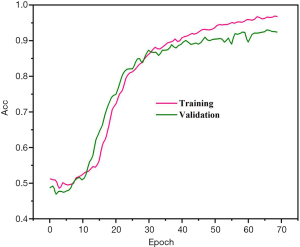
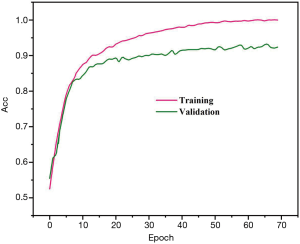
Precision, sensitivity, and specificity were considered the assessment metrics. Based on the obtained results, the best detection efficiency was observed in 1E−4 training rate. The suggested DPRNN network yielded a precision, sensitivity, and specificity of 88.31%, 84.84%, and 91.81%, respectively. Efficiencies of the proposed model in the presence and absence of the dropout layer are respectively depicted in Figures 3 and 4. Remarkably, it was possible for over-fitting to occur in the model without a dropout layer. As can be seen from Figure 3, there is no a considerable difference between the precision of the learning and testing datasets in the presence of the dropout layer. Meanwhile, Figure 4 shows the considerably different precision measures of the testing and learning datasets.
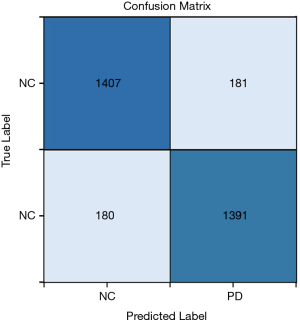
The confusion matrix of the obtained results is illustrated in Figure 5. According to this figure, 11.28% of the healthy cases were wrongly categorized into the PD class, while 11.49% of PD cases were classified incorrectly into the healthy class.
Discussion
An array of noninvasive methods have recently been suggested for the detection of PD, including those using voice (35-37) and gait (38). Also, various computer-aided methods have been proposed for obtaining proper models in order to differentiate between healthy and PD cases. For example, a feature reduction approach was proposed by Chen et al. (36) to remove the undesired data from the PD voice signals. These researchers obtained about 96.07% mean detection precision using the principal component analysis (PCA) reduction method and fuzzy k-nearest neighbor (FKNN) classification algorithm. Subsequently, Zuo et al. (37) increased the precision by applying a population-based optimization method on the FKNN classification method. This proposed method is used for the classification of the healthy versus Parkinson’s voices. In the study by Ma et al. (35), a hybrid method was proposed based on an extreme learning machine (ELM) method for differentiating Parkinson’s from healthy voices, which obtained a mean precision of 99.49%. Furthermore, a Fourier transform-based feature selection method was applied to distinguish the healthy and Parkinson’s gait signals (38). This proposed method resulted in 91.2% precision. Despite these attempts, few studies have used EEG signals for the detection PD. One experimental study (7) that did endeavor to diagnose PD cases by EEG signal found that the entropy levels of the PD EEG signal were considerably greater than those of healthy cases. Thus, the EEG signals related to PD have higher complexity (6). The higher order statistics (HOS) method also attempted to identify the diagnostic EEG features of PD. Results showed that the HOS method could explicitly present the hidden non-linear features of the PD EEG signals for the purposes of differentiation.
The present work proposes a deep RNN configuration for PD diagnosis. This proposed network contains a multitude layers to efficiently separate the PD from healthy cases by EEG signals. In addition, there is no requirement for manually obtained features in the proposed method. This distinction in the proposed method considerably reduces the number of procedural steps and allows for the optimal acquisition of the primary distinguishing features.
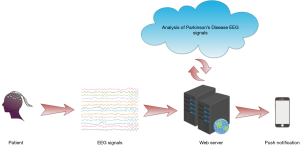
Furthermore, a web-based detection method was introduced for further enhancing the performance of the automated detection method, and may be investigated in future research. The procedure for this web-based automated method is illustrated in Figure 6. Network of detect is used in this method for detecting PD. The collected EEG signals are recorded in the local database in the clinic, and are forwarded via the cloud wherein our DRNN-based model is developed. Then, calculated results are sent back straight to the patients through phone messages. The use of this system can considerably decrease the workload of experts and clinicians.
The main novelties of the proposed method are summarized as follows:
- A deep RNN architecture equipped with LSTM units can automatically detect PD using EEG signals;
- The extraction, selection, and classification of the features is not required;
- A stratified 10-fold cross validation method is used for authentication of the model;
- This is the first time a deep learning method has been proposed to diagnose PD using EEG signals;
- Good diagnostic efficiency could be achieved even with a low number of healthy and PD cases, which shows good robustness of the proposed model;
Nevertheless, our proposed method and study may also exhibit the following limitations:
- A low number of cases (20 healthy and 20 PD cases) were used for developing the proposed PDRNN model;
- The proposed PDRNN model may have high computing costs in comparison with the traditional machine learning methods.
A high number of cases from various age/race ranges can be used to develop a more efficient model in future study. Moreover, the proposed model can be extended for diagnosis of other brain disease such as Alzheimer’s, autism, and depression disorders.
Conclusions
A novel computer-aided method based on a deep RNN network for the detection of PD by EEG signals was proposed. Based on our best knowledge, this is first time that this deep learning method has been applied for diagnosing PD by EEG signals. Although a low number of cases were studied in the present work, the proposed model could achieve good efficiency. This model yielded a precision, sensitivity, and specificity of 88.31%, 84.84%, and 91.81%, respectively. Due to high efficiency of the proposed model, it can be used as a reliable tool for the detection PD in the clinics. A larger number of the cases should be used to test and develop the proposed model in future research.
Acknowledgments
Funding: This work was funded by the Open Project Program of Key Laboratory of Tobacco Biology & Processing (201803), China National Tobacco Corporation Henan company (2018410000270035), Guizhou Tobacco Corporation Guiyang company (2016-07), China National Tobacco Corporation (110201002008, 110201402004).
Footnote
Reporting Checklist: The authors have completed the TRIPOD reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-5100
Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-5100
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-5100). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Medical Ethics Committee of Henan Provincial People’s Hospital (2019-031) and informed consent was taken from all the patients.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Stiles J, Jernigan TL. The basics of brain development. Neuropsychol Rev 2010;20:327-48. [Crossref] [PubMed]
- Silver J, Schwab ME, Popovich PG. Central nervous system regenerative failure: role of oligodendrocytes, astrocytes, and microglia. Cold Spring Harb Perspect Biol 2014;7:a020602. [Crossref] [PubMed]
- Paolini Paoletti F, Tambasco N, Parnetti L.. Levodopa treatment in Parkinson’s disease: earlier or later? Ann Transl Med 2019;7:S189. [Crossref] [PubMed]
- Oh SL, Hagiwara Y, Raghavendra U, et al. A deep learning approach for Parkinson’s disease diagnosis from EEG signals. Neural Computing and Applications 2018. [Crossref]
- World HO. Neurological disorders: public health challenges. World Health Organization 2006.
- Yuvaraj R, Rajendra Acharya U, Hagiwara Y. A novel Parkinson’s Disease Diagnosis Index using higher-order spectra features in EEG signals. Neural Computing and Applications 2018;30:1225-35. [Crossref]
- Han CX, Wang J, Yi GS, et al. Investigation of EEG abnormalities in the early stage of Parkinson’s disease. Cogn Neurodyn 2013;7:351-9. [Crossref] [PubMed]
- Gandal MJ, Edgar JC, Klook K, et al. Gamma synchrony: towards a translational biomarker for the treatment-resistant symptoms of schizophrenia. Neuropharmacology 2012;62:1504-18. [Crossref] [PubMed]
- Hampel H, Frank R, Broich K, et al. Biomarkers for Alzheimer’s disease: academic, industry and regulatory perspectives. Nat Rev Drug Discov 2010;9:560-74. [Crossref] [PubMed]
- Lima CA, Coelho AL, Chagas S. Automatic EEG signal classification for epilepsy diagnosis with Relevance Vector Machines. Expert Systems with Applications 2009;6:10054-9. [Crossref]
- Leuchter AF, Lesser IM, Trivedi MH, et al. An open pilot study of the combination of escitalopram and bupropion-SR for outpatients with major depressive disorder. J Psychiatr Pract 2008;14:271-80. [Crossref] [PubMed]
- Yuvaraj R, Murugappan M, Ibrahim NM, et al. Optimal set of EEG features for emotional state classification and trajectory visualization in Parkinson’s disease. Int J Psychophysiol 2014;94:482-95. [Crossref] [PubMed]
- Martis RJ, Acharya UR, Mandana KM, et al. Cardiac decision making using higher order spectra. Biomedical Signal Processing & Control 2013;8:193-203. [Crossref]
- Acharya UR, Chua EC, Chua KC, et al. Analysis and automatic identification of sleep stages using higher order spectra. Int J Neural Syst 2010;20:509-21. [Crossref] [PubMed]
- Chua KC, Chandran V, Acharya UR, et al. Analysis of epileptic EEG signals using higher order spectra. J Med Eng Technol 2009;33:42-50. [Crossref] [PubMed]
- Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks. Advances in neural information processing systems 2012.
- McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity. 1943. Bull Math Biol 1990;52:99-115, 73-97.
- Silver D, Huang A, Maddison CJ, et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016;529:484-9. [Crossref] [PubMed]
- Lusci A, Pollastri G, Baldi P. Deep architectures and deep learning in chemoinformatics: the prediction of aqueous solubility for drug-like molecules. J. Chem. Inf. Model. 2013;53:1563-75. [Crossref] [PubMed]
- Graves A, Mohamed AR, Hinton G, ^editors. Speech recognition with deep recurrent neural networks. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing; 2013.
- Pascanu R, Gulcehre C, Cho K, et al. How to Construct Deep Recurrent Neural Networks. 2013.
- Spadoto AA, Guido RC, Papa JP, et al. Parkinson’s disease identification through optimum-path forest. Conf Proc IEEE Eng Med Biol Soc 2010;2010:6087-90. [PubMed]
- Spadoto AA, Guido RC, Carnevali FL, et al. Improving Parkinson’s disease identification through evolutionary-based feature selection. Conf Proc IEEE Eng Med Biol Soc 2011;2011:7857-60. [PubMed]
- Soleimaniangharehchopogh F, Mohammadi P. A Case Study of Parkinson’s Disease Diagnosis using Artificial Neural Networks. International Journal of Computer Applications 2013;73:1-6. [Crossref]
- Pereira CR, Pereira DR, Silva FAD, et al. A step towards the automated diagnosis of parkinson’s disease: Analyzing handwriting movements. Proceedings of the IEEE Symposium on Computer Based Medical Systems 2015;2015:171-6.
- Weber SATU, Santos Filho CADU, Shelp AOU, et al. Classification of handwriting patterns in patients with Parkinson’s disease, using a biometric sensor. Global Advanced Research Journal of Medicine and Medical Sciences 2014;11:362-6.
- Peker M, Sen B, Delen D. Computer-Aided Diagnosis of Parkinson’s Disease Using Complex-Valued Neural Networks and mRMR Feature Selection Algorithm. J Healthc Eng 2015;6:281-302. [Crossref] [PubMed]
- Pereira CR, Pereira DR, Rosa GH, et al. Handwritten dynamics assessment through convolutional neural networks: An application to Parkinson’s disease identification. Artif Intell Med 2018;87:67-77. [Crossref] [PubMed]
- Acharya UR, Fujita H, Lih OS, et al. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network. Inform Sciences 2017;405:81-90. [Crossref]
- Acharya UR, Fujita H, Lih OS, et al. Automated detection of coronary artery disease using different durations of ECG segments with convolutional neural network. Knowl Based Syst 2017;132:62-71. [Crossref]
- Tan JH, Acharya UR, Bhandary SV, et al. Segmentation of optic disc, fovea and retinal vasculature using a single convolutional neural network. J Comput Sci Neth 2017;20:70-9. [Crossref]
- Bengio Y, Goodfellow IJ, Courville A. Deep learning, book in preparation for mit press. Disponıvel em 2015. Available online: https://mitpress.mit.edu/books/deep-learning
- Abedinia O, Amjady N, Ghasemi A. A new metaheuristic algorithm based on shark smell optimization. Complexity 2014.
- Hoehn MM, Yahr MD. Parkinsonism: onset, progression and mortality. Neurology 1967;17:427-42. [Crossref] [PubMed]
- Ma C, Ouyang J, Chen HL, et al. An efficient diagnosis system for Parkinson’s disease using kernel-based extreme learning machine with subtractive clustering features weighting approach. Comput Math Methods Med 2014;2014:985789. [Crossref] [PubMed]
- Chen HL, Huang CC, Yu XG, et al. An efficient diagnosis system for detection of Parkinson’s disease using fuzzy k-nearest neighbor approach. Expert Syst Appl 2013;40:263-71. [Crossref]
- Zuo WL, Wang ZY, Liu T, et al. Effective detection of Parkinson’s disease using an adaptive fuzzy fc-nearest neighbor approach. Biomedical Signal Processing & Control 2013;8:364-73. [Crossref]
- Daliri MR. Chi-square Distance Kernel Of The Gaits For The Diagnosis Of Parkinson’s Disease. Biomedical Signal Processing & Control 2013;8:66-70. [Crossref]