Gadoxetic acid-enhanced MRI radiomics signature: prediction of clinical outcome in hepatocellular carcinoma after surgical resection
Introduction
The second leading cause of cancer-specific mortality in the Asia-Pacific regions, and especially in China, is hepatocellular carcinoma (HCC). Surgical resection was recommended as primary treatment for patients at early stages by internationally endorsed guidelines (1). Nevertheless, over 70% of patients are still suffering from postoperative recurrence within five years, which is one of the main threats that lead to reduced survival (2,3). It is speculated that the recurrence of HCC was caused by either primary tumor metastasis or metachronous multicentric occurrence in the underlying liver disease (4-6).
Several pathological factors have been identified, such as poor tumor differentiation, microvascular invasion (MVI), satellite lesions to be associated with early recurrence in HCC (7,8). Background liver factors (e.g., advanced liver fibrosis or cirrhosis) have been considered as an essential host factor that causes multicentric recurrence of the remnant liver (9,10). However, these factors are available only postoperatively at the pathological examination of the surgical specimen. It is still challenging to find a useful tool that can reflect both intrahepatic metastasis and de novo carcinogenesis.
Medical imaging was commonly used in clinical procedures for HCC patients, and was stated to be closely associated with histopathological examination (11). Recent studies have focused on assessing the prognosis of patients with HCC by gadoxetic-acid enhanced MRI, with a variety of semantic imaging findings described (11-14). However, since conventional imaging evaluation relies on semantic features and provides relatively few metrics, the large quantity of additional useful information about tumor heterogeneity has been underutilized (15). Radiomics is a rapidly advancing form of medical image analysis, which enables the quantification of tumor phenotypic characteristics to provide prognostic information (16,17). By converting medical images into high-throughput imaging features, the radiomics method enables investigation for treatment monitoring and outcome prediction in the field of oncology (18-20). Several studies have assessed the prognostic aspect of radiomics signature in HCCs, with exceptional potential abilities for patient survival prediction and liver fibrosis diagnosis (21-24). However, most of published studies were in retrospective design and only focused on the intratumoral region (22,25). To our knowledge, few studies to date have tried to evaluate the tumor and non-tumorous liver tissues using a radiomics approach based on gadoxetic acid-enhanced MRI. Therefore, we hypothesized that this new method could be useful to predict survival outcome in HCC patients underwent hepatectomy.
In this study, we looked to develop and validate a radiomics-based nomogram that combined radiomics features and clinic-radiological predictors for preoperatively predicting overall survival (OS) in patients with HCC after surgical treatment.
We present the following article in accordance with the STROBE reporting checklist (available at http://dx.doi.org/10.21037/atm-20-3041).
Methods
Study population
This prospective study has obtained ethical approval from the institutional review board, and the informed consent from all patients was waived before patient enrollment. All patients underwent gadoxetic acid-enhanced MR imaging before surgery. Inclusion criteria were as follows: (I) age>18 years old; (II) patients suspected of having primary liver lesions based on clinical history, laboratory examinations and previous ultrasonography or CT results; (III) no treatment history, i.e., transcatheter arterial chemoembolization (TACE), radiofrequency ablation (RFA) or hepatectomy; (IV) no contraindication for MR examination. Demographic and clinicopathologic data were obtained from our hospital records.
Follow-up
Patients were followed up every three months during the first two years after surgery and then every six months regularly. All patients underwent contrast-enhanced CT or gadoxetic acid-enhanced MRI and serum AFP measurement. The endpoint of this study was OS, which was defined as the time from the date of surgery to the last follow-up or death. Patients were censored in July 2019 for living patients.
MR imaging techniques
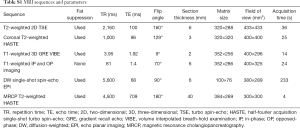
MR images of all patients were acquired on unform3.0T MR system (Magnetom Skyra, Siemens Healthcare, Erlangen, Germany) using an 18-channel body array coil. All patients underwent MR examination within one week before the operation and fasted for 6 to 8 hours before the examination. Baseline MR imaging sequences were composed of: (I) an breath-hold fat-suppressed T2-weighted imaging with fast spin-echo (FSE) sequence; (II) MR cholangiopancreatography (MRCP) heavily T2-weighted 2D imaging; (III) a diffusion-weighted imaging (DWI) (b values: 0, 50, 500, 800, 1,000, and 1,200 s/mm2). After administration of gadoxetic acid (Primovist®; Bayer Schering Pharma AG, Berlin, Germany), dynamic images in arterial phase (20–35 s), portal venous phase (60–70 s), transitional phase (3 min) and hepatobiliary phase (HBP) (20 min) were obtained using a fat-suppressed three-dimensional gradient-echo T1 weighted sequence (volume interpolated breath-hold examination, VIBE). A dose of 0.025 mmol/kg bodyweight of gadoxetic acid was injected intravenously at a rate of 2 mL/s, followed at once by a 30-mL saline flush. Detailed parameters of MR imaging sequences are provided in Table S1.
Full table
MR imaging findings
Two independent radiologists with 6 and 10 years of experience in abdominal imaging diagnosis, who were blinded to all clinical information and pathologic results, reviewed the MR images to evaluate the following imaging features: (I) tumor size; (II) multifocality; (III) smooth or non-smooth tumor margin; (IV) non-enhancing capsule; (V) arterial peritumoral enhancement; (VI) “washout”; (VII) peritumoral hypointensity on HBP images; and (VIII) signal intensity on HBP images. Any disagreements of the imaging features were resolved by consensus.
Regions of interest (ROI) segmentation and radiomics features extraction
An experienced radiologist (with five years of clinical experience in abdominal radiology) segmented ROIs on multiple phase images, including T2-weighted, non-enhanced T1-weighted, arterial phase, portal venous phase and HBP images, using in-house software (Analysis-Kit, version V3.0.0.R, GE healthcare).
Three different ROIs were delineated on each phase with the combination of automatic and manual approach by two different radiologists: first, ROI tumor were performed manually along the boundary of the tumor on the largest cross-sectional area; And then, a radius of 1cm surrounding the tumor boundary was automatically reconstructed based on the ROItumor, defined as ROIpenumbra; Finally, ROIliver was generated manually as a region of background liver parenchyma excluding ROI tumor and ROIpenumbra. Representative examples of image segmentation are shown in Figure 1. We extracted 350 radiomic features [20 histogram features, 40 texture features, 9 form factor features, 101 grey-level co-occurrence matrix (GLCM) features, and 180 grey-level run-length matrix (GLRLM) features] from each segmentation (background liver parenchyma, tumor, and its periphery), giving a total of 1050 features for every lesion.
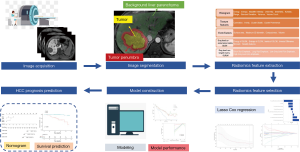
The image segmentation process was repeated by another experienced radiologist in 1 month to evaluate the interobserver reproducibility of the radiomic features by calculating the interclass correlation coefficient (ICC).
Statistical analysis
First, radiomics features with intraclass correlation coefficient >0.75 showed high stability and were kept for further analysis. Then, the least absolute shrinkage and selection operator (LASSO) Cox regression method was performed to select the most informative radiomics features from the primary cohort for building a radiomics signature (rad-score) (26). Ten-fold cross-validation was applied for parameters perfected and overfitting reduction. A rad-score for each patient was set up via a linear combination of the radiomics features weighted according to their respective coefficients.
Univariate and multivariate Cox regression analyses were used in the primary cohort to determine independent predictors of OS. Features with P value less than 0.05 in the univariate Cox regression were included in multivariate Cox regression models: (I) a clinic-radiological model, from clinic-radiological features; and (II) a combined model, from clinic-radiological features and radiomics signature. The final model was obtained based on a backward stepwise choice process by using Akaike’s information criterion.
Harrell's concordance index (C-index) was used to measure the discriminative ability of the proposed model in the primary cohort and confirmed in the validation cohort. Calibration curves were generated to assess the relationship between model-predicted probability and observed OS. Survival curves were created with the Kaplan-Meier method and compared using a two-sided log-rank test.
All statistical tests were performed using R version 3.5.2 (R Foundation for Statistical Computing, Vienna, Austria). A two-sided P value less than 0.05 was considered statistically significant.
Results
Patients characteristics
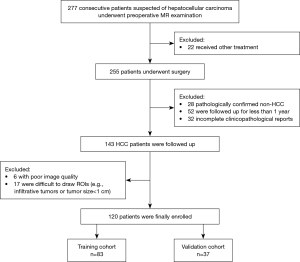
From July 2015 to May 2018, 277 consecutive patients with suspected HCC who underwent preoperative gadoxetic acid enhanced MR examination were included. Among them, 157 patients were excluded for the following reasons: (I) received other treatments instead of surgery, including trans-arterial chemoembolization (TACE) and RFA (n=22); (II) pathologically confirmed non-HCC (n=28); (III) patients lost to follow-up or were followed up for less than one year (n=52); (IV) poor image quality (n=6) and difficult tumor segmentation (n=17); (V) incomplete clinical or pathological data (n=32) (Figure 2). In total, 120 patients (mean age, 50.21±10.29 years; range, 28–77 years) were enrolled in the study, which was split into two cohorts: 83 patients who underwent surgery between July 2015 and August 2017 were divided into the primary cohort, while 37 patients who underwent surgery from August 2017 to May 2018 constituted the validation cohort.
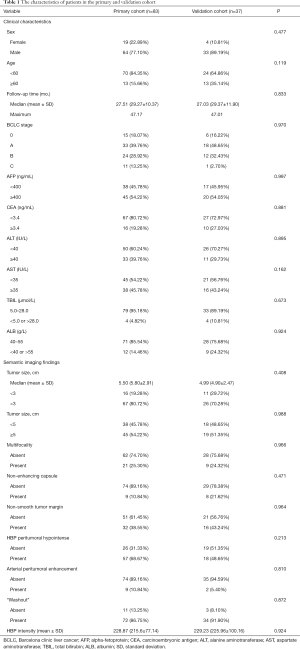
Table 1 summarized the characteristics of all patients in the primary and validation cohort. There was no significant difference between the primary and validation cohort (all P>0.05). The OS rate was 80.8% (97/120) for all patients. The median follow-up time was 27.51 months (range, 18.90–47.17 months) for the primary cohort and 27.03 months (range, 17.47–47.01 months) for the validation cohort.
Full table
Construction of radiomics signatures
In the primary cohort, radiomic features with nonzero coefficients were selected from multiple phases, MRI images, and quantitatively integrated into 3 rad-scores based on ROItumor, ROIliver, ROIpenumbra. Finally, all significant radiomics features were integrated into a combined rad-score. The calculation formulas of rad-scores were shown in the Supplementary file. Feature extraction algorithms can be found in Supplementary file.
Construction of survival models
In the univariate analysis, eight significant factors, including one clinical variable (BCLC stage), three semantic imaging features (non-enhancing capsule, arterial peritumoral enhancement, and non-smooth tumor margin) and 4 rad-scores were significantly associated with OS (all P<0.05).
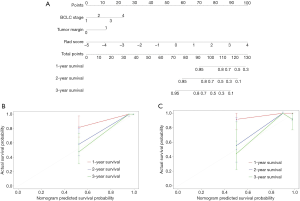
Multivariate Cox regression analyses confirmed BCLC stage [HR, 1.93; 95% confidence interval (CI), 0.91–4.12, P=0.09], non-smooth tumor margin (HR, 2.84; 95% CI, 0.88–9.16, P= 0.08) and combined rad-score (HR, 2.61; 95% CI, 1.71–3.96, P<0.001) as independent predictors of OS (Table 2). Based on coefficients assigned by multivariate Cox regression analysis, these independent predictors were combined linearly to set up the combined model presented as a nomogram (Figure 3A). Also, the BCLC stage and non-smooth tumor margin were used to construct the clinic-radiological model.

Full table
Performance of models
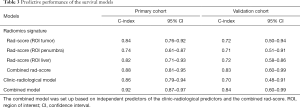
In the primary cohort, the combined rad-score derived from 3 ROIs yield the highest C-index of 0.88 (95% CI: 0.81–0.95), followed by the rad-score (ROItumor) (C-index, 0.84, 95% CI: 0.76–0.92), rad-score (ROI liver) (C-index, 0.82, 95% CI: 0.71–0.93) and rad-score (ROIpenumbra) (C-index, 0.74, 95% CI: 0.61–0.87). In the validation cohort, the C-index was 0.83 (95% CI: 0.60–0.99) for combined rad-score, 0.72 (95% CI: 0.50–0.94) for rad-score (ROItumor), 0.71 (95% CI: 0.51–0.91) for rad-score (ROIpenumbra) and 0.72 (95% CI: 0.58–0.86) for Rad-score (ROIliver), respectively. However, the pairwise comparison of 3 rad-scores based on 3 ROIs showed no significant differences in the primary and validation cohorts (all P>0.05).
After adding the combined rad-score into two clinic-radiological predictors, the combined model achieved better prognostic performance (C-index, 0.92, 95% CI: 0.87–0.97) than both the combined rad-score (C-index, 0.88, 95% CI: 0.81–0.95; P=0.016) and clinic-radiological model (C-index, 0.86, 95% CI: 0.79-0.94; P=0.039) in the primary cohort. Similar results were found in the validation cohort: the combined model yielded the highest C-index of 0.84 (95% CI: 0.60–0.99), compared with the combined rad-score (C-index, 0.83, 95% CI: 0.60–0.99) and clinic-radiological model (C-index, 0.70, 95% CI: 0.48–0.91) (Table 3). The calibration curves for the nomogram in predicting 1, 2, or 3 years survival rate after surgery in the primary and validation cohort are shown in Figure 3B,C.
Full table
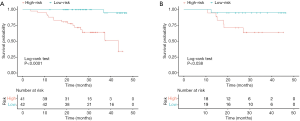
Patients were classified as low-risk or high-risk patients based on the cut-off values defined from the primary cohort. As shown in Figure 4, low-risk patients were significantly correlated with shorter postoperative survival in the primary cohort (log-rank test, P<0.0001; Figure 4A), which had been validated in the validation cohort (log-rank test, P=0.038; Figure 4B).
Discussion
In this study, we developed the radiomics signatures using gadoxetic acid-enhanced MRI radiomics features to predict survival outcomes in surgically resected HCC patients. The proposed radiomics signature could successfully distinguish high-risk from lower-risk survivors with HCC. By integrating radiomic and clinic-radiological features, the combined model showed improved predictive ability compared with the clinic-radiological model, suggesting that our findings could play a critical role in the clinical treatment management of HCC.
MVI is a well-known prognostic risk factor for early recurrence, highly correlated with tumor progression and more reduced postoperative survival, but is only microscopically detectable (27). Recent studies based on gadoxetic acid-enhanced MRI have indicated a significant association between MVI and semantic imaging features involving peritumoral tissue (including non-smooth tumor margin, arterial peritumoral enhancement, and peritumoral hypointensity on HBP). These features proved to be capable of predicting early recurrence of HCC after surgery, but with poor prognostic accuracy (AUC, 0.77–0.79) (7,28). Recently, the computational-based radiological imaging, known as radiomics, has shown promising ability in HCC prognostic prediction. Utilizing the radiomics method, we were able to capture either the tumor-related factors (e.g., intratumoral heterogeneity) or non-tumorous tissue factors (e.g., peritumoral or background liver status), and to assess the predictive accuracy among these tissues. These features extracted from the issues above could be efficiently selected and integrated to risk prediction models, which can offer essential information about HCC prognosis regardless of pathological information and predict the survival outcomes.
However, most of the earlier radiomic studies only evaluated the prognostic ability of radiomics features extracted from the intratumoral region. In the present study, we proposed a new approach to determine multi-scale radiomics features, from the intratumoral region (ROItumor), peritumoral region (ROIpenumbra), and background liver parenchyma (ROIliver). We defined ROI penumbra as a 1 cm expansion from the lesion based on the current surgical safety margin for HCC (29). As a result, 3 rad-scores were significantly associated with OS in the univariate analysis and showed comparable prognostic performances in both primary and validation cohorts. Among them, the Rad-score (ROIliver) showed outstanding prognostic performance with a C-index of 0.82 in the primary cohort and 0.72 in the validation cohort. Therefore, we suggested that changes in radiomics features from background liver parenchyma have predictive value in patient survival and might supply prognostic information related to recurrence and metastatic potential. Also, based on our findings, we found that the tumor was a more informative region than peritumoral tissue, with the higher prognostic performance observed. Our finding was in agreement with the one recent study based on CT images reporting that the radiomics features from the entire tumor were superior to those from the tumor edge zone in predicting MVI (30). Compared with CT-based study, our radiomics analysis based on gadoxetic acid-enhanced MRI has the advantages of higher soft-tissue contrast for more accurate tumor margin segmentation and also obtaining functional information of hepatocyte uptake from the tumor itself (31,32). In addition, after adding the radiomics features into a joint radiomics model, the combined rad-score demonstrated an improved performance with C-index of 0.88 in the training cohort and 0.83 in the validation cohort. It suggests that the multi-scale radiomics features involving different regions may have superior prognostic power for HCC patient survival prediction.
Also, the BCLC stage and non-smooth tumor margin were identified as independent predictors of OS in our study, which were consistent with previous studies (28,33). Although the BCLC staging system is commonly used for the clinical management guidance and prognostic prediction of HCC, the predictive accuracy of which may be limited by the lack of detailed quantitative parameters (34). Therefore, we further assessed the added value of quantitative radiomics features to the clinical management system and semantic imaging finding and setting up a multiscale model using several predictive factors from different aspects. The results of the combined model demonstrated proper calibration and discrimination ability in the primary and validation cohorts, and it is worth noting that the C-index of this model was higher than those of the other two prediction models (C-index, 0.92 for the primary cohort and 0.84 for the validation cohort), which suggests that the integration of quantitative radiomics features and clinic-radiological predictors within a computational framework could be a viable alternative in clinical practice.
Our study is still suffering from some limitations. First, the sample size of this study is limited to only 120 patients due to the prospective nature. However, all MR images used for our radiomics analysis were acquired in a uniform MR scanner with standardized sequences, protocols and reconstruction to avoid the bias of image. In the next step, large-scale samples based on multi-institutional cohort are necessary to facilitate the high-quality radiomics study. Second, 2D ROIs were applied in this study instead of 3D analysis, which enabled more effective tumor segmentation and were easy to achieve, and also proved to have a particular ability with 3D analysis (35). Additionally, the ROI of background liver parenchyma was not delineated on the largest cross-section of the liver, but the largest one of the tumor, which may limit the prognostic performance of background liver in our study. Third, all MR images in this prospective study were obtained with a uniform MR scanner at a single institution to reduce bias and variance of our results; our results still need further validation on its generalizability.
Conclusions
In conclusion, we showed the prognostic value of the radiomics-based risk model, integrating radiomic and clinic-radiological features, as a potent prognostic factor of HCC. Our model can supply the basis for alternative treatment strategy making and guide systematic follow-up, thus prolonging clinical outcome. Further studies on the integration of qualitative and quantitative image features were needed to confirm the efficiency and feasibility of our study.
Supplementary
Supplementary method
Supplementary table
The MR sequences included: a breath-hold fat-suppressed fast spin-echo T2-weighted imaging, and MR cholangiopancreatography (MRCP) heavily T2-weighted 2D imaging, and in- and opposed-phase gradient-echo T1-weighted sequence, a diffusion-weighted sequence (b values: 0, 50, 500, 800, 1,000, and 1,200 s/mm2), and a fat-suppressed 3D gradient-echo T1 weighted sequence (volume interpolated breath-hold examination, VIBE) before and after intravenous injection of Gd-EOB-DTPA at the arterial (bolus triggering, 7 s after the signal intensity of the celiac trunk was the highest), portal venous (60–70 s), transitional (3 min) and hepatobiliary phase (HBP, 20 min). The acquisition protocols were shown in Table S1.
Definition of image features
Histogram parameters
Histogram parameters are concerned with the properties of individual pixels. They describe the distribution of voxel intensities within the CT image through commonly used and basic metrics.
Energy
The energy feature measures the uniformity of the intensity level distribution. If the value is high, then the distribution is to a small number of intensity levels. Energy can be defined as:
|
| [1] |
Entropy
The entropy measures the randomness of the distribution of the coefficient values over the intensity levels. If the value of entropy is high, then the distribution is among more intensity levels in the image. This measurement is the inverse of energy. A simple image has low entropy, while a complex image has high entropy. Entropy can be defined as:
|
| [2] |
MaxIntensity
The maximum intensity value of X.
MinIntensity
The minimum intensity value of X.
MeanValue
The mean measures the average value of the intensity values.
|
| [3] |
Mean absolute deviation
The mean of the absolute deviations of all voxel intensities around the mean intensity value.
MedianIntensity
The median intensity value of X.
Range
The range of intensity values of X.
Root mean square (RMS):
|
| [4] |
Standard deviation
A measure that is used to quantify the amount of variation or dispersion of a set of data values.
|
| [5] |
where
Uniformity
|
| [6] |
Variance
Is the average of the squared differences from the Mean.
|
| [7] |
where
Volume count
Describe the size of the ROI.
Voxel value sum
Represents the Sum calculations for voxels in the ROI.
Relative deviation
Let
|
| [8] |
Frequency size
Quantiles
Quantile normalization is a global adjustment method that assumes the statistical distribution of each sample is the same. The normalization is achieved by forcing the observed distributions to be the same and the average distribution, which is obtained by taking the average of each quantile across samples. They are cut points dividing the range of a probability distribution into contiguous intervals with equal probabilities or dividing the observations in a sample in the same way.
For a finite population of N equally probable values indexed 1, …, N from lowest to highest, the k-th q-quantile of this population can equivalently be computed via the value of:
|
| [9] |
In A.K. software, we have 5 Quantiles: Quantile0.025, Quantil 0.25, Quantile0.5, Quantile0.75, Quantile0.975.
Percentiles
A percentile (or a centile) is a measure used in statistics indicating the value below which a given percentage of observations in a group of observations fall.
The percentile, p%, of a distribution is defined as that value of the brightness a such that: P(a) = p%.
or equivalently:
The P-th percentile 0<P≤100 of a list of N ordered values (sorted from least to greatest) is the smallest value in the list such that P percent of the data is less than or equal to that value. This is obtained by first calculating the ordinal rank and then taking the value from the ordered list that corresponds to that rank. The ordinal rank n is calculated using this formula:
|
| [10] |
A.K. software has 19 Percentiles: Percentile5, Percentile10, Percentile15, Percentile20, Percentile25, Percentile30, Percentile35, Percentile40, Percentile45, Percentile50, Percentile55, Percentile60, Percentile65, Percentile70, Percentile75, Percentile80, Percentile85, Percentile90, Percentile95.
Skewness
Represents the degree of asymmetric distribution in the image histogram; this means that in some distribution of data, the right and the left of the distribution are perfect mirror images of one another; the mean, median and mode are all measures of the center of a set of data. The Skewness of the data can be determined by how these quantities are related to one another.
“High values of Skewness” means that the distribution is asymmetric; otherwise the image is more symmetric; negative skew is when the numerical distribution is relatively long, also called negative Skewness distribution, the opposite is referred as positive Skewness distribution (positive skew). It’s possible to use the positive and negative Skewness to draw comparisons between the uniform distribution curve. The formula is:
|
| [11] |
where
Kurtosis
Kurtosis is a measure of whether the data are heavy-tailed or light-tailed relative to a normal distribution. That is, data sets with high kurtosis tend to have heavy tails or outliers. Data sets with low kurtosis tend to have light tails or a lack of outliers. A uniform distribution would be an extreme case.
When Kurtosis has small values, it shows more concentration; in contrast, when the Kurtosis is bigger is more dispersed. Usually, the size of positive and negative kurtosis is compared with the normal distribution curve. Positive Kurtosis indicates that the normal distribution curve is smoother; on the other hand, the negative Kurtosis indicates that the normal distribution is more precipitous. The formula is:
|
| [12] |
where
Texture parameters
The texture is one of the important characteristics used in identifying objects or regions of interest in an image, and texture represents the appearance of the surface and how its elements are distributed. It is considered an important concept in machine vision; in a sense, it assists in predicting the feeling of the surface (e.g., smoothness, coarseness…etc.) from the image. Various texture analysis approaches tend to represent views of the examined textures form different perspectives, and due to the multi-dimensionality of perceived texture, there is not an individual method that can be sufficient for all textures. Therefore, A.K. software is mainly concerned with texture classification accuracy improvement using textures features statistical-based methods.
Cluster shade
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (cluster) are more similar (in some sense or another) to each other than to those in other groups (clusters). It is a common technique for statistical data analysis.
Cluster shade: in clustered shading, we group similar view samples according to their position and, optionally, normal into clusters. In AK Software, we have the 18 parameters related to Cluster Shade. The formula is:
|
| [13] |
Cluster prominence
Cluster Prominence is a measure of the asymmetry of a given distribution; high values of this feature indicate that the symmetry of the image is low. In medical imaging, low values of cluster prominence represent a smaller peak for the image grey level value and usually, the grey level difference between the forms is small. The formula is:
|
| [14] |
Form factor parameters
These group of features includes descriptors of the three-dimensional size and shape of the tumor region. Let in the following definitions V denote the volume and A the surface area of the volume of interest. We determined the following shape- and size-based features:
- Sphericity
- Surface area
- Compactness 1
- Compactness 2
- Maximum 3D diameter
- Spherical disproportion
- Surfacetovolumeratio
- Volume
- VolumeCC and VolumeMM
|
| [15] |
The surface area is calculated by triangulation (i.e., dividing the surface into connected triangles) and is defined as:
|
| [16] |
|
| [17] |
|
| [18] |
The maximum three-dimensional tumor diameter is measured as the largest pairwise Euclidean distance between voxels on the surface of the tumor volume.
|
| [19] |
Where R is the radius of a sphere with the same volume as the tumor.
Where N is the total number of triangles covering the surface, and a, b and c are edge vectors of the triangles.
|
| [20] |
The volume (V) of the tumor is determined by counting the number of pixels in the tumor region and multiplying this value by the voxel size.
The maximum 3D diameter, surface area, and volume provide information on the size of the lesion. Measures of compactness, spherical disproportion, sphericity and the surface to volume ratio describe how spherical, rounded, or elongated the shape of the tumor is.
GLCM parameters
The Grey level co-occurrence matrix (GLCM) P (i, j|θ, d) represents the joint probability of certain sets of pixels having certain grey-level values. It calculates how many times a pixel with grey-level i occurs jointly with another pixel having a grey value j. By varying the displacement vector d between each pair of pixels.
The advantage of the co-occurrence matrix calculations is that the co-occurring pairs of pixels can be spatially related in various orientations with reference to distance and angular spatial relationships, as on considering the relationship between two pixels at a time. As a result, the combination of grey levels and their positions are exhibited apparently. Therefore, it is defined as “A two-dimensional histogram of gray levels for pair of pixels, which are separated by a fixed spatial relationship.” However, the matrix is sensitive to rotation, with the change of different offsets defining pixel relationships by varying directions, including the rotation angle of an offset: 0°, 45°, 90°, 135° and displacement vectors (distance to the neighbor pixel: 1, 2, 3 ..), different co-occurrence distributions from the same image of reference. GLCM of an image is computed using displacement vector d defined by its radius (distance or count to the next adjacent neighbor which preferably is equal to one) and rotational angles.
Energy of GLCM
This feature returns the sum of squared elements in the GLCM, with range = [0, 1]. Energy is 1 for a constant image and is high when image has very good homogeneity or when pixels are very similar. The Property Energy is also known as uniformity, uniformity of energy, and angular second moment. In A.K. Software, we have 18 parameters related to GLCM Energy. The formula is:
|
| [21] |
Where g is a GLCM, i, j are the spatial coordinates of g (i, j).
Entropy of GLCM
Entropy is a measure of randomness of intensity image. Entropy shows the amount of information of the image that is needed for image compression. Entropy measures the loss of information or message in a transmitted signal and also measures the image information. In A.K. Software, we have the 18 parameters related to the GLCM Entropy. The formula is:
|
| [22] |
Inertia of GLCM
It reflects the clarity of the image and texture groove depth. The contrast is proportional to the texture groove. High values of the groove produce more clarity. In contrast, small values of the groove will result in small contrast and fuzzy image. In A.K. Software, we have the 18 parameters related to the Inertia. The formula is:
|
| [23] |
Correlation
Correlation measures the similarity of the grey levels in neighboring pixels, tells how correlated a pixel is to its neighbor over the whole image, with range = [−1, 1]. Correlation is 1 or −1 for a perfectly positively or negatively correlated image. In A.K. Software, we have the 18 parameters related to the Correlation. The formula is:
|
| [24] |
Inverse difference moment
Inverse Difference Moment (IDM) is the local homogeneity. It is high when the local gray level is uniform and inverse GLCM is high. IDM weight value is the inverse of the Contrast weight. The formula is:
|
| [25] |
Haralick features
Haralick correlation
Measures the degree of similarity of the gray level of the image in the row or column direction. Represents the local grey level correlation, the greater its value, the greater the correlation. The formula is:
|
| [26] |
Angular second moment
|
| [27] |
Contrast
The contrast feature is a different moment of the P matrix and is a measurement of the contrast or the number of local variations present in the image.
|
| [28] |
Haralick entropy
|
| [29] |
Hara variance
|
| [30] |
Sum average
|
| [31] |
Sum variance
|
| [32] |
Sum Entropy
|
| [33] |
Difference variance
Equals to the variance of px-y.
Difference entropy
|
| [34] |
Inverse difference moment
|
| [35] |
GLRLM parameters
The grey level run-length matrix (GLRLM) Pr (i, j|θ) is defined as the numbers of runs with pixels of gray level i and run length j for a given direction θ. GLRLMs is generated for each sample image segment having directions (0°,45°,90° & 135°), then the following ten statistical features were derived: short run emphasis, long run emphasis, grey level non-uniformity, run length non-uniformity, Low Grey Level Run Emphasis, High Grey Level Run Emphasis, Short Run Low Grey Level Emphasis, Short Run High Grey Level Emphasis, Long Run Low Grey Level Emphasis and Long Run High Grey Level Emphasis.
Short run emphasis
|
| [36] |
Long run emphasis
|
| [37] |
Grey level non-uniformity
|
| [38] |
Run length non-uniformity
|
| [39] |
Low grey level run emphasis
|
| [40] |
High grey level run emphasis
|
| [41] |
Short run low grey level emphasis
|
| [42] |
Short run high grey level emphasis
|
| [43] |
Long run low grey level emphasis
|
| [44] |
Long run high grey level emphasis
|
| [45] |
where nr is the total number of runs, and np is the number of pixels in the image.
Acknowledgments
Funding: The authors express their gratitude to the Research Grant of National Nature Science Foundation of China (Grant number 81771797) and the 1.3.5 project for disciplines of excellence, West China Hospital, Sichuan University (Grant number ZYJC18008) for grant support.
Footnote
Reporting Checklist: The authors have completed the STROBE reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-3041
Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-3041
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-3041). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This prospective study has obtained ethical approval from the institutional review board (2016 No. 297), and the informed consent from all patients was waived before patient enrollment.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Omata M, Cheng AL, Kokudo N, et al. Asia-Pacific clinical practice guidelines on the management of hepatocellular carcinoma: a 2017 update. Hepatol Int 2017;11:317-70. [Crossref] [PubMed]
- Imamura H, Matsuyama Y, Tanaka E, et al. Risk factors contributing to early and late phase intrahepatic recurrence of hepatocellular carcinoma after hepatectomy. J Hepatol 2003;38:200-07. [Crossref] [PubMed]
- Chawla A, Ferrone C. Hepatocellular carcinoma surgical therapy: perspectives on the current limits to resection. Chin Clin Oncol 2018;7:48. [Crossref] [PubMed]
- Poon RT, Fan ST, Ng IOL, et al. Different risk factors and prognosis for early and late intrahepatic recurrence after resection of hepatocellular carcinoma. Cancer 2000;89:500-07. [Crossref] [PubMed]
- Ye L, Liang R, Zhang J, et al. Postoperative albumin-bilirubin grade and albumin-bilirubin change predict the outcomes of hepatocellular carcinoma after hepatectomy. Ann Transl Med 2019;7:367. [Crossref] [PubMed]
- Nenu I, Breaban I, Pascalau S, et al. The future is now: beyond first line systemic therapy in hepatocellular carcinoma. Transl Cancer Res 2019;8:S261-74. [Crossref]
- An C, Kim DW, Park YN, et al. Single Hepatocellular Carcinoma: Preoperative MR Imaging to Predict Early Recurrence after Curative Resection. Radiology 2015;276:433-43. [Crossref] [PubMed]
- Zhou YM, Yang JM, Li B, et al. Risk factors for early recurrence of small hepatocellular carcinoma after curative resection. Hepatobiliary Pancreat Dis Int 2010;9:33-7. [PubMed]
- Sasaki Y, Imaoka S, Masutani S, et al. Influence of coexisting cirrhosis on long-term prognosis after surgery in patients with hepatocellular carcinoma. Surgery 1992;112:515-21. [PubMed]
- Cai W, He B, Hu M, et al. A radiomics-based nomogram for the preoperative prediction of posthepatectomy liver failure in patients with hepatocellular carcinoma. Surg Oncol 2019;28:78-85. [Crossref] [PubMed]
- Inoue M, Ogasawara S, Chiba T, et al. Presence of non-hypervascular hypointense nodules on Gadolinium-ethoxybenzyl-diethylenetriamine pentaacetic acid-enhanced magnetic resonance imaging in patients with hepatocellular carcinoma. J Gastroenterol Hepatol 2017;32:908-15. [Crossref] [PubMed]
- Lee S, Kim KW, Jeong WK, et al. Gadoxetic acid-enhanced MRI as a predictor of recurrence of HCC after liver transplantation. Eur Radiol 2020;30:987-95. [Crossref] [PubMed]
- Kim DK, An C, Chung YE, et al. Hepatobiliary versus Extracellular MRI Contrast Agents in Hepatocellular Carcinoma Detection: Hepatobiliary Phase Features in Relation to Disease-free Survival. Radiology 2019;293:594-604. [Crossref] [PubMed]
- Woo JH, Song KD, Kim SH, et al. Subcentimeter hypervascular nodules with typical imaging findings of hepatocellular carcinoma on gadoxetic acid-enhanced MRI: Outcomes of early treatment and watchful waiting. Eur Radiol 2017;27:4406-14. [Crossref] [PubMed]
- Bi WL, Hosny A, Schabath MB, et al. Artificial intelligence in cancer imaging: clinical challenges and applications. CA Cancer J Clin 2019;69:127-57. [PubMed]
- Wakabayashi T, Ouhmich F, Gonzalez-Cabrera C, et al. Radiomics in hepatocellular carcinoma: a quantitative review. Hepatol Int 2019. [Crossref] [PubMed]
- Gillies RJ, Kinahan PE, Hricak H. Radiomics: images are more than pictures, they are data. Radiology 2016;278:563-77. [Crossref] [PubMed]
- Florez E, Fatemi A, Claudio PP, et al. Emergence of Radiomics: Novel Methodology Identifying Imaging Biomarkers of Disease in Diagnosis, Response, and Progression. SM J Clin. Med. Imaging 2018;4:1019.
- Lai-Kwon J, Siva S, Lewin J. Assessing the Clinical Utility of Computed Tomography-Based Radiomics. Oncologist 2018;23:747-9. [Crossref] [PubMed]
- Gardin I, Gregoire V, Gibon D, et al. Radiomics: Principles and radiotherapy applications. Crit Rev Oncol Hematol 2019;138:44-50. [Crossref] [PubMed]
- Park HJ, Lee SS, Park B, et al. Radiomics Analysis of Gadoxetic Acid-enhanced MRI for Staging Liver Fibrosis. Radiology 2019;290:380-7. [Crossref] [PubMed]
- Brenet Defour L, Mule S, Tenenhaus A, et al. Hepatocellular carcinoma: CT texture analysis as a predictor of survival after surgical resection. Eur Radiol 2019;29:1231-9. [Crossref] [PubMed]
- Chen S, Zhu Y, Liu Z, et al. Texture analysis of baseline multiphasic hepatic computed tomography images for the prognosis of single hepatocellular carcinoma after hepatectomy: A retrospective pilot study. Eur J Radiol 2017;90:198-204. [Crossref] [PubMed]
- Miranda Magalhaes Santos JM, Clemente Oliveira B, Araujo-Filho JAB, et al. State-of-the-art in radiomics of hepatocellular carcinoma: a review of basic principles, applications, and limitations. Abdom Radiol (NY) 2020;45:342-53. [Crossref] [PubMed]
- Zheng BH, Liu LZ, Zhang ZZ, et al. Radiomics score: a potential prognostic imaging feature for postoperative survival of solitary HCC patients. BMC Cancer 2018;18:1148. [Crossref] [PubMed]
- Tibshirani R. The lasso method for variable selection in the Cox model. Stat Med 1997;16:385-95. [Crossref] [PubMed]
- Eguchi S, Takatsuki M, Hidaka M, et al. Predictor for histological microvascular invasion of hepatocellular carcinoma: a lesson from 229 consecutive cases of curative liver resection. World J Surg 2010;34:1034-8. [Crossref] [PubMed]
- Lee S, Kim S H, Lee J E, et al. Preoperative gadoxetic acid-enhanced MRI for predicting microvascular invasion in patients with single hepatocellular carcinoma. J Hepatol 2017;67:526-34. [Crossref] [PubMed]
- Wang ZX, Jiang CP, Cao Y, et al. Preoperative serum liver enzyme markers for predicting early recurrence after curative resection of hepatocellular carcinoma. Hepatobiliary Pancreat Dis Int 2015;14:178-85. [Crossref] [PubMed]
- Xu X, Zhang HL, Liu QP, et al. Radiomic analysis of contrast-enhanced CT predicts microvascular invasion and outcome in hepatocellular carcinoma. J Hepatol 2019;70:1133-44. [Crossref] [PubMed]
- Choi JW, Lee JM, Kim SJ, et al. Hepatocellular carcinoma: imaging patterns on gadoxetic acid-enhanced MR Images and their value as an imaging biomarker. Radiology 2013;267:776-86. [Crossref] [PubMed]
- Kim S, Shin J, Kim DY, et al. Radiomics on Gadoxetic Acid-Enhanced Magnetic Resonance Imaging for Prediction of Postoperative Early and Late Recurrence of Single Hepatocellular Carcinoma. Clin Cancer Res 2019;25:3847-55. [Crossref] [PubMed]
- Kim BK, Kim SU, Park JY, et al. Applicability of BCLC stage for prognostic stratification in comparison with other staging systems: single centre experience from long-term clinical outcomes of 1717 treatment-naïve patients with hepatocellular carcinoma. Liver International 2012;32:1120-7. [Crossref] [PubMed]
- Vitale A, Burra P, Frigo AC, et al. Survival benefit of liver resection for patients with hepatocellular carcinoma across different Barcelona Clinic Liver Cancer stages: a multicentre study. J Hepatol 2015;62:617-24. [Crossref] [PubMed]
- Shen C, Liu Z, Guan M, et al. 2D and 3D CT Radiomics Features Prognostic Performance Comparison in Non-Small Cell Lung Cancer. Transl Oncol 2017;10:886-94. [Crossref] [PubMed]