
Imitation dynamics in the mitigation of the novel coronavirus disease (COVID-19) outbreak in Wuhan, China from 2019 to 2020
Introduction
The coronavirus disease 2019 (COVID-19) was first identified in Wuhan, China on December 2019 in patients presenting with atypical pneumonia and is considered life-threatening (1,2). Common symptoms of the infection include fever, cough and shortness of breath (3). Since December 31 of 2019, Wuhan has officially released the situation report of the outbreak of COVID-19. The cumulative number of officially reported cases remained constant at 41 cases until January 15, and rapidly increased afterward (4,5). As of February 6 (11:59 PM, GMT+8), the still ongoing outbreak has resulted in a reported 28,139 (10,117 in Wuhan) confirmed cases including 564 (414 in Wuhan) deaths and 1,344 (459 in Wuhan) discharges in mainland China (4). Sporadic cases exported from Wuhan were reported in many Asian, Oceanian, North American and European countries or regions (6), and the case number is still increasing, which suggests travel-related spreading risks as indicated by (7-12).
A number of studies used modelling techniques to explore and project the trends of the COVID-19 outbreak. By using the number of exported cases, a research group at the Imperial College London estimated that there had been 1,723 (95% CI: 427−4,471) infections in Wuhan by January 12 and this would increase to 4,000 (95% CI: 1,000−9,700) by January 18. They also estimated the basic reproduction number (R0) to be 2.6 (95% CI: 1.5−3.5) (13). Leung et al. drew a similar conclusion and estimated the number of cases exported from Wuhan to other major cities in China (14). Most existing estimates of the R0 of COVID-19 lie between 1.5 and 4 (10,13,15-19), and is in the same scale as the other two well-known coronavirus diseases: severe acute respiratory syndrome (SARS) and Middle East respiratory syndrome (MERS) (20-22).
The ‘city-lockdown’ policy was firstly implemented in Wuhan and suspended all public traffic within the city and all inbound and outbound transportations from or to Wuhan as of January 23, 2020 (23). Similar policies were also implemented in many other Chinese cities subsequently. This effectively reduced the spatial spreading of the COVID-19 in terms of the number of exported cases domestically and internationally, but the city-level (within each isolated city) outbreaks remain a major concern to be addressed.
With increasing public information about COVID-19 and outbreak released since the second half of January 2020, see Box 1, there has been an increasing number of individuals at risk seeking healthcare supports most commonly in the form of self-administered disease infection prevention actions, i.e., infection risk averse actions. And by the first week of February, most people in the cities seriously affected by COVID-19 chose to take infection prevention actions. On the one hand, taking disease control actions can reduce the morbidity and mortality risks involved with the COVID-19 outbreak. However, on the other hand, the infection prevention actions are usually very constraining and difficult to adhere to, and involve giving up to some degree of a normal lifestyle. For example, they may include major mobility restrictions, the continuous wearing of uncomfortable facemasks, frequent cleaning and sterilization, and there is also the financial and mental ‘cost’ required to implement these kinds of measures. Due to the many possible ‘losses’ in utility associated with disease infection prevention actions, this contradiction between choice of actions makes the elimination difficult under a voluntary acting scheme. There is clearly a clash between the optimal choice of action for the individual and the coverage of infection prevention actions uptake that is best for the population as a whole. In other words, the total coverage of infection prevention actions uptake under a voluntary policy is the collective result of individual decisions to take or not to take actions. Similar to the game theory of vaccination proposed in the literature (27), when this coverage increases, an increasing number of ‘free-rider’ individuals will no longer have the incentive to take control actions, since non-action-takers can enjoy the herd immunity without suffering the costs associated with the strict infection prevention actions. This game theoretical contradiction in vaccination decision-making is a well-known phenomenon (27-30).

During the outbreak, the action-taking game evolves through time, and individuals cannot precisely determine their probability and possible (negative) consequences of becoming infected.
Moreover, people adopt updated information and new strategies through learning, by imitating others who appear to have adopted more successful strategies (31). Hence, an imitation dynamical behavior with a learning process between individuals, is proposed, which captures the evolutionary process of the frequencies of strategic choices in the population, with respect to disease infection prevention actions. In this study, we develop a compartmental epidemic model incorporated with a behavioral imitation through a game theoretical decision-making process in order to study the dynamics of COVID-19 outbreak in Wuhan, China. We project the future trends and patterns of this outbreak in Wuhan under the most realistic settings. From a public health control viewpoint, we explore the probable courses of the outbreak in terms of size and timing under several public interventions in improving public awareness and sensitivity to the infection risk as well as their potential impact.
Methods
Surveillance data
Due to late reporting or under reporting of the cases in the situation reports in the early outbreak (5,32), which is also indicated by (10,13,16), the officially reported time series data of cases will introduce biases into the estimation and simulation without reasonable adjustment for varying reporting rates (19,33,34). Therefore, we adopt the time series of laboratory confirmed cases from Li et al. (15). All cases were laboratory confirmed following the case definition by the National Health Commission of China (35) indicated in (15). Specifically the cases ‘were collected onto standardized forms through interviews of infected persons, relatives, close contacts, and health care workers’, and aggregated by the date of symptoms onset (15). The data should cover most of symptomatic pneumonia of unknown etiology if not all from December 1, 2019 to early January 8, 2020. We choose to use the data up to January 8, one day before the decline of epidemic curve in Figure 1 of (15), for model fitting and parameter estimation. The decline after January 8, 2020 in their figure was ‘likely to be due to delays in diagnosis and laboratory confirmation’ (15).
Game of taking infection prevention actions
Due to the emergency of the COVID-19 outbreak in Wuhan, a number of infection prevention actions were promoted to individuals at risk, including wearing facemasks, maintaining hand hygiene and reducing outdoor mobility (or activities), etc. Existing literatures suggest that these infection prevention actions could well have reduced the risk of infection in past outbreaks of infectious diseases (22,36). The model of “imitation dynamics” presented here was previously used for predicting the decision-making of vaccination uptake to prevent pediatric infections during the vaccine scare era (27,37). We develop an imitation behavioral modelling framework of two types of strategies for individuals:
- those willing to take disease infection prevention actions associated with a payoff at E0, and
- those not willing to take disease infection prevention actions associated with a payoff at E1.
For each individual, we assume that his or her willingness (or probability) to take disease infection prevention actions, denoted by p, is controlled by the payoff profile (E0 and E1) and the sensitivity of this payoff profile (κ), as explained shortly.
Considering the possibility of being infected, denoted by Φ ranging from 0 to 1, during an outbreak, we account for the prevalence of infections, denoted by I/N. Since N is the total population size and fixed to be a constant, we model Φ as an increasing function of I, i.e., Φ(I). If we denote r0 (>0) as the cost of being infected by COVID-19, the payoff for an individual that does not take infection prevention actions is given by Eq. [1]:
|
| [1] |
For an individual who takes infection prevention actions, the possibility of being infected is reduced by a scalar α, and the possibility is αΦ. At the same time, the cost for taking infection prevention actions is r1, which is expected to be much smaller than r0, i.e., r1 << r0. Thus, the payoff for an individual that takes infection prevention actions is given by Eq. [2]:
|
| [2] |
The payoff gains for one not taking infection prevention actions who then switches to the strategy of taking infection prevention actions is ΔE, such that
|
| [3] |
Since r1 << r0, we rescale the ΔE by r0 and define r = r1/r0 such that 0 < r < 1 and r is expected being close to 0. With the tradeoff of the game holding, we have the scaled ΔE, denoted by Δe, in Eq. [4].
|
| [4] |
As Φ(I) measures the risk of being infected, it is proportional to the force of infection that is approximately the product of transmission rate (β) and the instantaneous prevalence rate (I), i.e., Φ(I) is proportional to βI/N. Since the β usually is a constant and its effects can be controlled by other terms, we simply define Φ(I) = I/N throughout this study.
For the imitation dynamics, it is assumed that individuals randomly sample other members of the population at a constant rate. If the strategy of the sampled members provides a higher payoff, then the strategy is adopted with a probability proportional to the expected gain in payoff. Let p denote the probability of an individual who is willing to take infection prevention actions. We further model the imitation rate, K (>0), at which individuals sample others and switch strategies, as a function of Δe, i.e., K(Δe). Therefore, the time evolution of p is given by Eq. [5].
|
| [5] |
Since K(Δe) is expected to be an increasing function with respect to Δe, for simplicity, we further define K(Δe) = κΔe. The term κ is a proportionality constant that controls the sensitivity of the imitation rate in response to the perceived payoff gain (Δe). Thus, Eq. [5] can be refined as in Eq. [6].
|
| [6] |
As the term κ controls the sensitivity of the imitation rate in response to the perceived payoff gain, larger κ means that the population is more sensitive to be motivated to take the disease prevention infection prevention actions. When the prevalence of infections (I/N) increases, the combined imitation rate (κΔe) will also increase. The term Δe is the payoff gain, and it measures the ‘cost’ (risk) of being infected due to lack of infection prevention actions based on the real-world facts. The sensitivity term (κ) adjusts and rescales this cost level (Δe) from the public perception side.
Epidemic model
We develop a compartmental model based on the classic susceptible-exposed-infectious-recovered (‘SEIR’) modelling structure. The susceptible population is separated into two groups of population, and they are the people not taking infection prevention actions, denoted by U, and the people taking infection prevention actions, denoted by M. The infectious population is denoted by I, and the removed (by recovery or death) population denoted by R. In addition to the classic compartmental framework, we include the game of taking infection prevention actions or not in the model by allowing switching status (of the action-taking strategy) between U and M at a considerably large rate, ξ.
The switching status is also controlled by the probability of willingness to take infection prevention actions (p) as modelled in Eq. [6]. Hence, we have the following epidemic model as in Eq. [7].
|
| [7] |
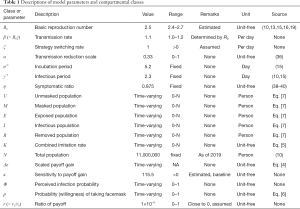
The total population N = U + M + E + I + R is a constant. The descriptions of model parameters and the associated references are summarized in Table 1.
Full table
Reproduction numbers
At the disease-free equilibrium, with initially 100% of the population in the ‘U’ class, the basic reproduction number can be formulated as R0 = β/γ, by using the next generation matrix approach (41). Using the same technique, the time-varying effective reproduction number can be defined as Reff = R0(U + αM)/N.
Fitting framework
We fit the model (6) to the daily number of cases collected in (15), and incorporate with a symptomatic ratio, denoted by η, to only fit the symptomatic infections to the observed data. We model the theoretical value of daily number of symptomatic cases, zi, for the i-th day as in Eq. [8].
|
| [8] |
Following previous studies (10,42), with the observed daily number of symptomatic cases denoted by ci for the i-th day, the likelihood can be calculated under a Poisson distribution with rate at zi, and denoted by Li(ci|zi). Therefore, the overall likelihood for parameter estimation can be formulated as in Eq. [9]:
|
| [9] |
Here, Θ denotes the vector of parameters to be estimated, ci is the observation from the data, and zi is defined in Eq. [8] and regarded as the theoretical value of ci. The Li(·) is the Poisson distribution for the i-th day, and thus namely, the measurement noises are addressed by the Poisson-distributed likelihood framework.
The stochastic variant of the model simulation is implemented as a continuous-time Markov process approximated via a multinomial process with a fixed time step of 0.1 day. We estimate the model parameters by maximizing the likelihood function defined in Eq. [9], as well as by comparing the key modelling outcomes of the outbreak in Wuhan with Wu et al. (10). Following previous studies (19,42-46), the 95% confidence intervals (95% CI) of estimates are obtained by using the profile likelihood approach with the Chi-squared quantile as the cutoff threshold (47). We conduct 1,000 simulation samples and calculate the median and 95% CI.
Initial condition
Since this is the first outbreak of COVID-19 in history, we assume the initial susceptible population is relatively large, and take it to be 100% as of December 1, 2019. This means that U(0) = N − 1, and we set the 1 infection as the seed at the start of the outbreak. The initial value of p is taken to be 0.01, that is, only 1% of the population was willing to take infection prevention actions at the early stage of the outbreak.
Simulation schemes under different scenarios
We explore the impacts of the changes in
- sensitivity to payoff gain (κ), and
- effectiveness of control measures (measured by α).
This will include examining how theses parameters affect the epidemiological features of the COVID-19 outbreak in Wuhan, including
- peak size (as in incidence rate);
- final size (in percentage infection), and
- timing of effective control (i.e., the first time at which Reff <1).
The baseline scenario is the fitting results with the maximum likelihood estimates of each parameter summarized in Table 1. We vary κ by per 10-fold change for 5 times, and thus this means we have 6 settings including 0-fold (baseline), 10-, 100-, 1,000-, 10,000- and 100,000-fold increase in κ. Similarly, we vary α by per 0.5-fold change for 3 times, and thus this means we have 4 settings including 0-fold (baseline), 1/2-, 1/4- and 1/8-fold decrease in α. Therefore, we have (6×4=) 24 different scenarios including the baseline.
We select a scenario regarding κ that is most approaches to the real situation for further simulation analysis. The timing of key outbreak-related information released that were concentrated at the second half of January 2020, see Box 1. Hence, p is expected to start increasing since the second half of January 2020. Referring to the real-world fact, almost every people in Wuhan and elsewhere affected by increasing number of cases is willing to take or has already took infection prevention actions against COVID-19. Thus, p is also expected to approach 1 in the first week of January. By examining the trends of the time-varying p, we consider a scenario regarding κ that has the desired changing dynamics of p as an approximation of the real-world situation. Details of the κ selection can be found in Supplementary files.
The disease surveillance data during the early phase of the outbreak were obtained from Li et al. (15).
Results
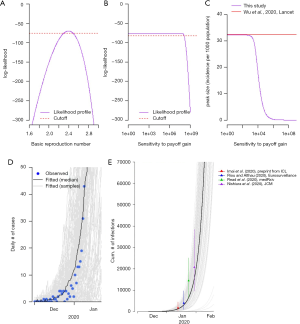
We estimated the basic reproduction number, R0, at 2.5 (95% CI: 2.4−2.7), see Figure 1A, which is consistent with previous estimates from 1.5 to 4 (10,13,15-19). Although the sensitivity to the payoff gain, κ, does not have significant difference to the data from early outbreak, see Figure 1B, we choose the baseline value of κ by comparing the estimated peak size with the previous estimate in Wu et al. (10). As shown in Figure 1C, when κ becomes larger than 115.5, the estimated peak size starts to become lower than the previous estimate in (10), and thus we treat κ =115.5 as the baseline value. Figure 1D shows the fitting results to the symptomatic cases data published in (15) at the early phase of the outbreak. Figure 1E shows the comparison between our simulation on cumulative number of infections and those from other literatures (9,13,16,17), and they are largely in line with each other.
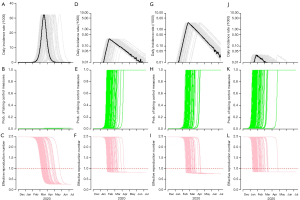
Figure 2 summarizes the simulation results under different scenarios with, from left to right, 0-fold (baseline), 1,000-, 10,000- (the most realistic) and 100,000-fold increase in κ. The simulated epidemic curve under the baseline scenario, in Figure 2A, is consistent with that in the Figure 4 of Wu et al. (10). The fold-increase in κ is likely to mitigate the COVID-19 outbreak in terms of peak level and total infections, see top panels in Figure 2. The middle panels in Figure 2 show the changing dynamics of the willingness (or probability) to take infection prevention actions, i.e., the time-varying p in Eqn (5). This time evolution of p is expected to be largely associated with the situation of the outbreak-related information spread and individuals’ behaviors. By examining the changing dynamics of p, we select the scenario in Figure 2D with 10,000-fold of the baseline κ as an approximation of the real situation, and this scenario will also be used for further simulation analysis. Details of and more reasoning on the selection of scenarios can be found in Supplementary files. For the bottom panels in Figure 2, we found the point in time when Reff first reduces below unity, i.e., Reff <1, which implies the epidemic curve will decrease. Figure 2 shows this point in time becomes earlier as κ increase. This finding implies that increasing the sensitivity to take infection risk averse actions would help control the epidemic efficiently.
We summarized the estimates of the key outbreak features under real-world approximation as highlighted in Table 2. We estimate the peak size at 0.28 (95% CI: 0.24−0.32) infections per 1,000 population in Wuhan. The final size of the outbreak is likely to infect 1.35% (95% CI: 1.00−2.12%) of the whole population in Wuhan, see Figure 2D. The outbreak is likely to be under control in terms of the Reff <1 on February 9 (95% CI: January 31−March 27), 2020. By multiplying the sensitivity of taking infection risk averse actions (κ) by an additional 10-fold (from the real situation), the peak size is likely to reduce at 0.03 (95% CI: 0.03−0.03) infections per 1,000 population, and the final size at 0.15% (95% CI: 0.10−0.22%). However, if κ decreases 10-fold from the real situation, the peak size is likely to rise at 2.65 (95% CI: 2.29−3.07) infections per 1,000 population, and the final size at 10.53% (95% CI: 8.35−13.69%).

Full table
In Table 2, we also project the outbreak features under several derivative scenarios from the real-world approximation. These ‘what if’ scenarios allow us to evaluate the effect of a certain factor of interest on mitigating the COVID-19 outbreak. By holding other factors unchanged, if the effectiveness of the control measures increases by 2-fold, which means the term α is reduced to be 1/2-fold of its baseline value, the peak size will be likely to reduce to 0.20 (95% CI: 0.17−0.24) infections per 1,000 population in Wuhan, and the final size at 0.40% (95% CI: 0.36−0.46%).
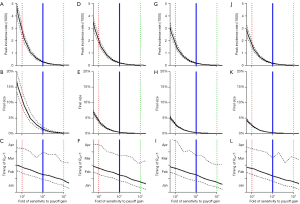
Although we find that the timing of the disease under control (i.e., Reff <1) is unlikely to change significantly even by increasing as much as 8-fold in the effectiveness of the control measures, see bottom panels in Figure 3, the outbreak size can be successfully reduced, see top and middle panels in Figure 3. The estimates shown in Figure 3 also allow us to further check the sensitivity of results and explore the impacts of varying κ and α on the outbreak features. Both increasing κ and decreasing α are likely to mitigate the COVID-19 outbreak scale in Wuhan.
Discussion
The R0 of COVID-19 is estimated at 2.5 that is in the same magnitude as many other well-known respiratory infections, including SARS and pandemic influenza H1N1 in 2009 (22,48). We estimate there will be some 148.5 (95% CI: 110.0−233.2) thousand infections under the most realistic scenario (i.e., with 10,000-fold of κ from its baseline) by the end of May 2020, given a total of 11 million population in Wuhan. The outbreak will most likely peak in the first half of February (which matches the fact that the daily new confirmations started showing a sign of decreasing these days), and eventually drop to a level of daily new infections of 10 in June 2020, see Figure 2D.
The compartmental model we adopted is similar to those used by other researchers (8,10,13,16,18,19,49-53). Thus, our analyses are based on validated baseline model and approaches and our estimated characteristics are consistent with previous estimates, see Figure 1C,E. Our modelling framework incorporates human reaction and behavior change to the risk and allows us to understand and evaluate the effects of these factors on mitigating the outbreak. We demonstrate that increasing the level of public awareness (in terms of κ) would significantly reduce the outbreak size, see Table 2. Increasing public perception to avert infection risk (κ) and willingness to take infection prevention actions (p) would be helpful to mitigate the on-going COVID-19 outbreak. To achieve this, substantial measures that improve public awareness and willingness for self-protection are strongly desired at the earliest phase locally and domestically. Timely outbreak information updates are crucial. Prevention actions (e.g., avoiding risky contacts and reducing their frequency, avoiding gatherings, and working at home), i.e., moving from class U to M in model (6), would drastically reduce transmission rates, i.e., reduction from β to αβ, As more individuals becoming willing to take actions, the supply and quality of the resources and well-being in supporting for the implementation of the infection prevention actions, become important issues. For example, the availability, cost, quality and quantity of the necessary equipment, e.g., facemask and alcohol sterilizer, sufficient room for self-quarantine and routine supply during mobility restriction, e.g., food and power, are crucially needed to win the combat.
This study has limitations. Our model simulation is conducted under the assumption that the resource for infection prevention actions, e.g., facemasks, can be sufficiently supplied once demanded. This may not always be true during the outbreak, especially when the demand from the population rapidly increase (reflected by p), see Figure 2K,N. However, it appears the charity contribution of the disease prevention resources, which currently occurs in mainland China to support the ‘anti-COVID-19’ campaign in Wuhan, is to some extent alleviating this problem of ‘lack of resources’. Thus, our results still provide legitimate insights on projection and forecasting of the outbreak. Our analysis did not include extreme changes from the side of healthcare providers, e.g., public health service, hospital and use of new drugs or vaccine. Previous modelling analysis demonstrated that large improvement in COVID-19 infection detecting and development and coverage of effective vaccination would reduce the number of cases from the theoretical point of view (53). The timely infections detection associated with isolation could decrease the effective infectious period (γ−1) of transmission, and effective mass vaccination would largely reduce the susceptible pool (U + M). Although these improvements in public health service would mitigate the outbreak by reducing Reff, the development procedure and delivery of such services or products may be time consuming. Hence, we note that the large changes in healthcare services and products commonly requires relatively long period of time for clinical testing and evaluation, and thus it is unlike to bring significant impacts to current situation. As also pointed out by Wu et al. (10), ‘precisely what and how much should be done is highly contextually specific and there is no one-size-fits-all set of prescriptive interventions that would be appropriate across all settings’. Our imitation framework considers the improvement in the human reaction to take infection risk averse measures in a self-sustaining manner, which demonstrates only by increasing the level of public awareness would largely reduce the outbreak size, see top panels of Figure 3. With the knowledges of the detailed travelling patterns, the number and timing of seed infections in other localities, our modelling framework can be extended to a complex metapopulation version to explore the outbreaks on a spatial level. We remark that as shown in Figure 2 of Wu et al. (10), the outbreak patterns in different places in China are almost the same in peak size, final size and timing of peak as that generated by our model here.
Supplementary
Selection of the scenario regarding κ for the real-world situation
In the main text, we vary κ by per 10-fold change for 5 times including 0-fold (baseline), 10-, 100-, 1,000-, 10,000- and 100,000-fold increase in κ for simulation. Figure S1 summarizes the simulation results under different scenarios with 0-fold (baseline), 10-, 100-, 1,000-, 10,000- and 100,000-fold increase in κ. The fold-increase in κ is likely to mitigate the 2019-nCoV outbreak in terms of peak level and total infections, see top panels in Figure S1.

The middle panels in Figure S1 show the changing dynamics of the willingness (or probability) to take infection prevention actions, i.e., the time-varying p. We select a scenario regarding κ that is most approaches to the real situation for further simulation analysis. The timing of key outbreak-related information released that were concentrated at the second half of January 2020, see Box 1 in the main text. Hence, p is expected to start increasing since the second half of January 2020. Referring to the real-world fact, almost everyone in Wuhan and elsewhere affected by increasing number of cases is willing to take or has already took infection prevention actions against 2019-nCoV. Thus, p is also expected to approach 1 in the first week of January. Therefore, we consider a scenario regarding κ that has the desired changing dynamics of p as an approximation of the real-world situation. By examining the trends of the time-varying p in the middle panels of Figure S1, we confirm that the scenario in Figure S1N associated with 10,000-fold of the baseline κ is probably the closest to the real-world situation. Therefore, we regard this scenario as an approximation of the real situation for further simulation analysis in the main text.
The bottom panels of Figure S1 show the changing dynamics of the Reff, and we found increasing κ will shorten the period to control the outbreak in terms of the first date when Reff <1 occurs. We remark that the results of 0-fold (baseline), 1,000-, 10,000- and 100,000-fold are same as in the main results, but only in different scale and sequence.
Acknowledgments
The authors would like to acknowledge colleagues for helpful comments.
Funding: DH was supported by General Research Fund (Grant Number 15205119) of the Research Grants Council (RGC) of Hong Kong, China and Alibaba (China)-Hong Kong Polytechnic Collaborative Research project. LS was supported by an ARC grant DP170102303.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm.2020.03.168). Dr. He reports grants from Alibaba (China), during the conduct of the study. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- World Health Organization. 'Pneumonia of unknown cause – China', Emergencies preparedness, response, Disease outbreak news, World Health Organization (WHO). 2020. Available online: https://www.who.int/csr/don/05-january-2020-pneumonia-of-unkown-cause-china/en/
- Wu P, Hao X, Lau EH, et al. Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan, China, as at 22 January 2020. Eurosurveillance 2020;25:2000044. [Crossref] [PubMed]
- Huang C, Wang Y, Li X, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020;395:497-506. [Crossref] [PubMed]
- National Health Commission of the People’s Republic of China. 'Situation report of the pneumonia cases caused by the novel coronavirus', released by the National Health Commission of the People’s Republic of China (in Chinese). 2020. Available online: http://www.nhc.gov.cn/yjb/s3578/202001/a3c8b5144067417889d8760254b1a7ca.shtml
- Wuhan municipal health commission. 'News press and situation reports of the pneumonia caused by novel coronavirus', from December 31, 2019 to Janunary 21, 2020 released by the Wuhan municipal health commission, China. 2020. Available online: http://wjw.wuhan.gov.cn/front/web/list2nd/no/710
- World Health Organization. Novel Coronavirus (2019-nCoV) situation reports, released by the World Health Organization (WHO). 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports
- Bogoch II, Watts A, Thomas-Bachli A, et al. Pneumonia of unknown etiology in Wuhan, China: potential for international spread via commercial air travel. J Travel Medicine 2020. [Crossref]
- Lai S, Bogoch I, Ruktanonchai N, et al. Assessing spread risk of Wuhan novel coronavirus within and beyond China, January-April 2020: a travel network-based modelling study. medRxiv 2020:2020.02.04.20020479.
- Nishiura H, Kobayashi T, Yang Y, et al. The Rate of Underascertainment of Novel Coronavirus (2019-nCoV) Infection: Estimation Using Japanese Passengers Data on Evacuation Flights. J Clin Med 2020. [Crossref] [PubMed]
- Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet 2020;395:689-97. [Crossref] [PubMed]
- Zhao S, Zhuang Z, Ran J, et al. The association between domestic train transportation and novel coronavirus outbreak in China, from 2019 to 2020: A data-driven correlational report. Travel Med Infect Dis 2020. [Crossref] [PubMed]
- Zhao S, Zhuang Z, Cao P, et al. Quantifying the association between domestic travel and the exportation of novel coronavirus (2019-nCoV) cases from Wuhan, China in 2020: A correlational analysis. J Travel Med 2020. [Crossref] [PubMed]
- Imai N, Dorigatti I, Cori A, et al. Estimating the potential total number of novel Coronavirus (2019-nCoV) cases in Wuhan City, China. Preprint published by the Imperial College London 2020.
- Leung K, Wu JT, Leung GM. Nowcasting and forecasting the Wuhan 2019-nCoV outbreak Preprint published by the School of Public Health of the University of Hong Kong 2020. Available online: https://files.sph.hku.hk/download/wuhan_exportation_preprint.pdf
- Li Q, Guan X, Wu P, et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N Engl J Med 2020. [Epub ahead of print]. [Crossref] [PubMed]
- Read JM, Bridgen JR, Cummings DA, et al. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv 2020:2020.01.23.20018549.
- Riou J, Althaus CL. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Euro Surveill 2020. [Crossref] [PubMed]
- Shen M, Peng Z, Xiao Y, et al. Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China. bioRxiv 2020:2020.01.23.916726.
- Zhao S, Musa SS, Lin Q, et al. Estimating the Unreported Number of Novel Coronavirus (2019-nCoV) Cases in China in the First Half of January 2020: A Data-Driven Modelling Analysis of the Early Outbreak. J Clin Med 2020. [Crossref] [PubMed]
- Bauch CT, Lloyd-Smith JO, Coffee MP, et al. Dynamically modeling SARS and other newly emerging respiratory illnesses: past, present, and future. Epidemiology 2005;16:791-801. [Crossref] [PubMed]
- Lin Q, Chiu AP, Zhao S, et al. Modeling the spread of Middle East respiratory syndrome coronavirus in Saudi Arabia. Stat Methods Med Res 2018;27:1968-78. [Crossref] [PubMed]
- Lipsitch M, Cohen T, Cooper B, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003;300:1966-70. [Crossref] [PubMed]
- The government of Wuhan. The headquarters notice of the noval coronavirus (2019-nCoV) infection of pneumonia epidemic prevention and control, the government of Wuhan, China. 2020. Available online: http://www.wuhan.gov.cn/2019_web/whyw/202001/t20200123_304072.html
- World Health Organization. Laboratory testing for 2019 novel coronavirus (2019-nCoV) in suspected human cases: Interim guidance, released on January 17, 2020 by the World Health Organization (WHO). Available online: https://www.who.int/publications-detail/laboratory-testing-for-2019-novel-coronavirus-in-suspected-human-cases-20200117
- Parry J.. China coronavirus: cases surge as official admits human to human transmission. BMJ 2020;368:m236. [Crossref] [PubMed]
- World Health Organization. Statement on the second meeting of the International Health Regulations Emergency Committee regarding the outbreak of novel coronavirus (2019-nCoV), World Health Organization (WHO). 2020. Available online: https://www.who.int/news-room/detail/30-01-2020-statement-on-the-second-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov)
- Bauch CT. Imitation dynamics predict vaccinating behaviour. Proc Biol Sci 2005;272:1669-75. [Crossref] [PubMed]
- Bauch CT, Earn DJ. Vaccination and the theory of games. Proc Natl Acad Sci U S A 2004;101:13391-4. [Crossref] [PubMed]
- Fine PE, Clarkson JA. Individual versus public priorities in the determination of optimal vaccination policies. Am J Epidemiol 1986;124:1012-20. [Crossref] [PubMed]
- Geoffard PY, Philipson T. Disease Eradication: Private versus Public Vaccination. American Economic Review 1997;87:222-30.
- Eksin C, Shamma JS, Weitz JS. Disease dynamics in a stochastic network game: a little empathy goes a long way in averting outbreaks. Sci Rep 2017;7:44122. [Crossref] [PubMed]
- National Health Commission of China. An outbreak situation update on the pneumonia caused by the novel coronavirus (2019-nCoV) infection, National Health Commission of China. 2020. Available online: http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml
- Zhao S, Lin Q, Ran J, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int J Infect Dis 2020;92:214-7. [Crossref] [PubMed]
- Tuite AR, Fisman DN. Reporting, Epidemic Growth, and Reproduction Numbers for the 2019 Novel Coronavirus (2019-nCoV) Epidemic. Ann Intern Med 2020. [Epub ahead of print]. [Crossref] [PubMed]
- National Health Commission of the People’s Republic of China. 'Definition of suspected cases of unexplained pneumonia', the National Health Commission of the People’s Republic of China (in Chinese). 2020. Available online: http://www.nhc.gov.cn/
- Cowling BJ, Chan KH, Fang VJ, et al. Facemasks and hand hygiene to prevent influenza transmission in households: a cluster randomized trial. Ann Intern Med 2009;151:437-46. [Crossref] [PubMed]
- Wang Z, Bauch CT, Bhattacharyya S, et al. Statistical physics of vaccination. Phys Rep 2016;664:1-113. [Crossref]
- Al-Tawfiq JA, Gautret P. Asymptomatic Middle East Respiratory Syndrome Coronavirus (MERS-CoV) infection: Extent and implications for infection control: A systematic review. Travel Med Infect Dis 2019;27:27-32. [Crossref] [PubMed]
- Chan JF, Yuan S, Kok KH, et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet 2020;395:514-23. [Crossref] [PubMed]
- Wilder-Smith A, Teleman MD, Heng BH, et al. Asymptomatic SARS coronavirus infection among healthcare workers, Singapore. Emerg Infect Dis 2005;11:1142-5. [Crossref] [PubMed]
- van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 2002;180:29-48. [Crossref] [PubMed]
- Zhao S, Lou Y, Chiu APY, et al. Modelling the skip-and-resurgence of Japanese encephalitis epidemics in Hong Kong. J Theor Biol 2018;454:1-10. [Crossref] [PubMed]
- Breto C, He D, Ionides EL, et al. Time series analysis via mechanistic models. Ann Appl Stat 2009;3:319-48. [Crossref]
- Earn DJ, He D, Loeb MB, et al. Effects of School Closure on Incidence of Pandemic Influenza in Alberta, Canada. Ann Intern Med 2012;156:173-81. [Crossref] [PubMed]
- He D, Gao D, Lou Y, et al. A comparison study of Zika virus outbreaks in French Polynesia, Colombia and the State of Bahia in Brazil. Sci Rep 2017;7:273. [Crossref] [PubMed]
- He D, Ionides EL, King AA. Plug-and-play inference for disease dynamics: measles in large and small populations as a case study. J R Soc Interface 2010;7:271-83. [Crossref] [PubMed]
- Fan J, Huang T. Profile likelihood inferences on semiparametric varying-coefficient partially linear models. Bernoulli 2005;11:1031-57. [Crossref]
- Cowling BJ, Fang VJ, Riley S, et al. Estimation of the serial interval of influenza. Epidemiology 2009;20:344. [Crossref] [PubMed]
- Du Z, Wang L, Cauchemez S, et al. Risk of 2019 novel coronavirus importations throughout China prior to the Wuhan quarantine. medRxiv 2020:2020.01.28.20019299.
- Linton NM, Kobayashi T, Yang Y, et al. Epidemiological characteristics of novel coronavirus infection: A statistical analysis of publicly available case data. medRxiv 2020:2020.01.26.20018754.
- Liu T, Hu J, Kang M, et al. Transmission dynamics of 2019 novel coronavirus (2019-nCoV). bioRxiv 2020:2020.01.25.919787.
- Riou J, Althaus CL. Pattern of early human-to-human transmission of Wuhan 2019-nCoV. bioRxiv 2020:2020.01.23.917351.
- Chowell G, Dhillon R, Srikrishna D. Getting to zero quickly in the 2019-nCov epidemic with vaccines or rapid testing. medRxiv 2020:2020.02.03.20020271.


