Effect of overhang and stiffness on accessibility of catheter tip to lung defects under surgical constraints
Introduction
Pneumothorax is a collapsed lung due to an unusual collection of air in the chest cavity. The symptoms of pneumothorax include chest pain and difficulty breathing. Ruptured bullae or blebs that create an air-leaking point on a lung constitutes one of the major causes of pneumothorax (1). The air-leaking point due to rupturing is referred to as the lung defect in this paper. To control air leakage, several techniques, such as bullectomy, wedge resection of blebs, and ligation of bullae have been utilized (2). Pleural symphysis has also been performed to prevent recurrence by executing visceral pleural coverage or chemical and mechanical pleurodesis.
In cases in which patients are expected to be at high risk of postoperative complications from an operation under general anesthesia or postoperative prolonged air leakage, carrying out a surgical intervention can be unsafe. Minimally-invasive surgery using a catheter is often recommended for such patients. Fibrin glue application under pleurography (FGAP) is a minimally-invasive surgery technique to treat air leakage caused by ruptured bullae (3,4). This procedure provides the fibrin sealant Tisseel (Baxter Healthcare Corp., Deerfield, IL, USA), which is a viscous fluid that blocks the air-leaking point, to the lung defects through a catheter, as shown in Figure 1 (4).
The most important aspect of a successful pneumothorax surgery using a catheter is controlling the distal end’s position and angle with respect to the location of a lung defect in order to deliver Tisseel to the exact location. However, precise tip positioning is very challenging during the operation, and this leads to numerous problems. Much trial and error is requisite to position the tip to the exact spot, which makes the operation greatly inconvenient. Specifically, the operator is required to spend too much time on one patient. Moreover, Tisseel is wasted if it is dropped in the wrong area, leading to significant financial losses. This is also stressful for both the operator and the patients.
An effective operation method for tip positioning has not yet been developed for pneumothorax surgery. Currently, the FGAP operation proceeds with a pigtail catheter or a small bore catheter (5,6). A chest tube is placed in pleural space in advance and set still, and then a catheter is inserted through the chest tube (Figure 1). Next, the overhang is adjusted, the length of the catheter is extended beyond the chest tube, and an appropriate rotation angle is determined. The rotation is made about the central axis of the tube’s cross-section by turning the proximal handle. Although currently the FGAP operation is not commonly employed, the procedure is very effective for patients who cannot tolerate conventional surgery. However, the biggest challenge of this method is tip positioning of the catheter. Much repetition is normally needed before tip positioning is successfully achieved. Consequently, a superior method for tip positioning is requisite.
Using a steerable catheter, rather than a pigtail catheter, could dramatically improve the target accessibility of the catheter’s tip. The tip positioning of a steerable catheter is affected by overhang, flexural rigidity of each segment of the catheter, and pull-wire tension. These three parameters are interconnected in a complex manner through nonlinear beam deflection equations. Therefore, predicting and controlling the tip position and angle are challenging.
The extant literature has developed methods for controlling the tip of a steerable catheter. For example, one study uses a kinematic model to predict the tip position, assuming the catheter as a pseudo-rigid cantilever beam subjected to bending moment (7). Another investigation developed a control formula that obtains the required pull-wire tension in order to position a catheter’s tip to the target location (8). Although numerous other studies have analyzed the deflection of catheters, they usually focus on other types of catheters. The two above-mentioned studies specifically examine deflection of a wire-driven steerable catheter. Unfortunately, even though these two researches can successfully control and predict the tip position of a catheter, they are unsuitable for pneumothorax surgery in that they only analyze the deflection of the distal shaft and not the entire tube. This is only applicable for operations in which the configuration of the proximal shaft is fixed, such as in cardiovascular interventions. Indeed, attempting to study the entire bending of a steerable catheter with these methods is very difficult because the analysis becomes prohibitively complex. Moreover, the configuration of the entire catheter tube changes in FGAP, and this necessitates an examination of the bending of the entire tube.
In the authors’ previous study, a simulation tool that implements a nonlinear deflection curve of a multi-segmented steerable catheter was developed to identify the required pull-wire tension for positioning a catheter’s tip to the desired location (9). This simulation tool could analyze the entire catheter’s deflection with multiple segments of various stiffnesses. This previous study, however, did not consider the effect of a chest tube that substantially constrains the deflection of a catheter.
This paper presents a method that enhances the target accessibility of the catheter tip by predicting the required overhang, flexural rigidity, and pull-wire tension via implementing a simulation tool developed based on Euler-Bernoulli nonlinear beam theory. Furthermore, theoretical analysis is performed to renovate the simulation tool to reflect the deflection of a catheter constrained by a chest tube. The effect of overhang and catheter stiffness on the deflection configuration of a catheter is investigated to evaluate catheter tip accessibility to the different lung defect locations. This simulation tool can assist medical doctors not only to select the best catheter prior to operation, but also to control the catheter to reach the lung defect with the indicated pull-wire tension and overhang.
Methods
Accessibility of catheter tip to various lung defect locations
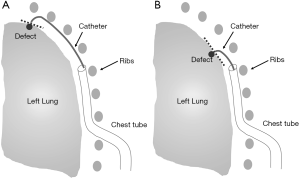
Figure 1 shows different possible configurations of a catheter and a chest tube in the FGAP operation. Depending on the location of the defect, e.g., apex or azygo-esophageal recess (Figure 1) (10,11), the required catheter tip position and angle are determined. The catheter tip should be positioned in such a way that minimizes the distance to the defect and is 90° relative to the tangent plane of the defect. The distance and relative angle are chosen as accessibility indices to evaluate the tip accessibility of a catheter to the lung defect.
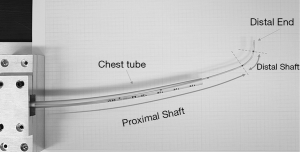
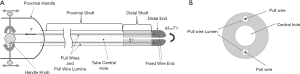
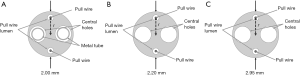
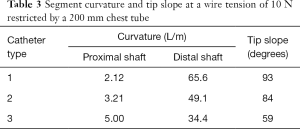
The structure of a steerable catheter is shown in Figure 2. The steerable catheter comprises a proximal shaft of hard material with relatively high stiffness and a distal shaft of soft material with relatively low stiffness so that the former can convey the distal shaft in a straight line as possible with little deflection while the latter can easily reach a defective area with a lot of deflection. The distal end made of hard material is attached at the very end. Since the stiffness and the length of each segment can vary depending on catheter type, the deforming behaviors are different for different catheters. Thus, certain catheters can have better accessibility to designated locations than others. The optimal catheter selection can be made by considering the stiffness of each segment and the location of the defect. Three available catheters are evaluated using the accessibility indexes in this paper. Their cross-sections are presented in Figure 3. The stiffness of each catheter by segment is summarized in Table 1. The table is providing the lengths and flexural rigidities of each segment. After selecting the best catheter, the position and the angle of the catheter tip can be controlled by manipulating the overhang and the pull-wire tension. First, the overhang is adjusted, and then an appropriate pull-wire tension is applied to bring the catheter to an optimal configuration for a specified defect location.

Full table
Simplified catheter deflection model constrained by a chest tube
Exact model
Generally, a steerable catheter is bent when bending moment, MT, created by tension T and distance r, is applied (Figure 2). The current authors suggested a solution of free catheter deflection as a nonlinear large deflection of cantilever beam without constraint in a previous work (9). From Eq. [1], a nonlinear beam deflection formula, Eq. [2] was derived, where EI is the flexural rigidity of the catheter, L is the length of the catheter, x is the horizontal coordinate, and y is the length of the vertical deflection at the corresponding x value. The constant curve length s, shown in Eq. [3], has to restrict Eq. [2] to generate an accurate curve (12). Based on these equations, catheter deflection simulation without a chest tube was developed in the current authors’ previous study (9).
|
| [1] |
|
| [2] |
|
| [3] |
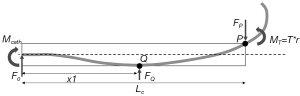
Catheter deflection becomes limited by the chest tube during actual surgeries. As the catheter bends inside of a chest tube of length Lc, the catheter comes into contact with the tip of the chest tube at point P (Figure 4). The chest tube begins to deflect along with the catheter due to a point load FP. The opposing reaction force of FP exerted on the catheter, illustrated in Figure 4, constrains the deflection of the catheter. The magnitude of FP can be determined by matching the amount of the vertical deflection of the catheter and the chest tube.
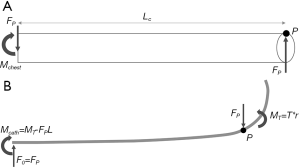
Eqs. [4] and [5] are derived from Eq. [1] and by applying the cantilever beam conditions shown in Figure 4. EIo and EIi is the flexural rigidity of the chest tube and the catheter, respectively, and yo and yi is the vertical deflection of the chest tube and the catheter, respectively. Eqs. [4] and [5] become constrained by the curve length formula shown in Eqs. [6] and [7], respectively, where so is the curve length of the chest tube, and si is the curve length of the catheter.
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
An additional contact point between the catheter and the chest tube is generated in the middle of the chest tube at point Q as the catheter deflects more (Figure 5). x1 is the length from the edge of the chest tube to point Q. Point load FQ is created, and the deflection of the catheter is restricted to an even greater extent as the free body diagram of the catheter inside of the chest tube in Figure 5 manifests. The requisite pull-wire tension to reach this phase varies depending on the type of catheter and overhang length. Moreover, both FQ and x1 values change as the pull-wire tension increases. Accurate deflection curves can also only be simulated prior to this phase, which is very limiting. Consequently, the simulation model becomes too complicated, and thus such a model is infeasible. A simplified model needs to be developed for these reasons.
Simplified model
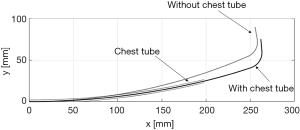
In the simplified model, the segment of the catheter within the chest tube and the chest tube itself are considered as a single segment with higher stiffness. The length of the remaining proximal shaft outside of the chest tube varies by overhang. Deflection is analyzed as free deflection using Eqs. [2] and [3]. An accurate simulation result of the constrained deflection of the catheter can be generated based on these equations. Figure 6 shows the effect of the chest tube by comparing the simulation results of the deflected catheter with and without the chest tube. The tips of the two catheters are approximately 15 mm apart at a pull-wire tension of 8 N, which is a significant amount.
Results
Experimental setup and results
A deformation experiment is conducted to evaluate the reliability of the simplified model. Simulation error is measured as a key performance indicator. A low simulation error means that tip positioning can be controlled well according to the simulation results, and this makes the surgery much more effective. Deformation experiments are repeated five times to obtain the mean value of the experimental results. The mean value is used to compare with the simulation result for calculating the error. The maximum standard deviation of the experimental results at the tip occurred at the highest pull-wire tension, and was calculated to be approximately 3.7 mm. This means that the probability that the lung defect will be located within 5 mm from the tip of the catheter is greater than 82%. This confirms the reproducibility of the deformation experiments.
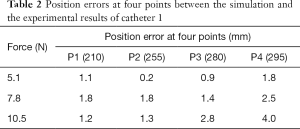
The chest tube used in this study is 200 mm long, and has an inner diameter of 6 mm and outer diameter of 8 mm. The flexural rigidity of the chest tube is 1.98×10−3 Nm2. Figure 7 presents a test setup, in which catheters inserted through a chest tube are tested to acquire their deflected curves under various wire tensions. The deflected curve shape of a catheter is recorded by measuring the displacement of four pre-selected points at 210, 255, 285, and 295 mm along the catheter tube. A 1 mm resolution graph paper that lies beneath the catheter is utilized to measure the displacement of these points. Multiple tests are carried out under different wire tensions.
The test is performed with catheter 1. The experimental results and simulation of the simplified model are compared in Figure 8. The simplified model achieves results that are close to the experimental data until a pull-wire tension of 10.5 N. Simulation errors of the simplified model for each wire tension are listed in Table 2. The maximum position error of 4 mm occurs at 10.5 N, which is reasonable for the purpose of FGAP.
Full table
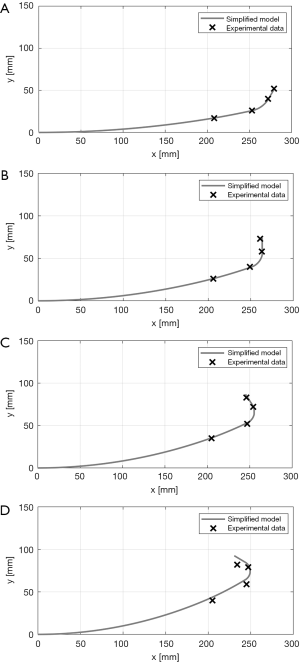
The simulation result reveals a substantial error at a wire tension of 12.8 N, as shown in Figure 8D. The gap between the tips of the simulation and the actual catheter is more than 10 mm. The experimental result shows much less bending at the chest tube area than that of the simulation result. This might be due to the effect of a complex interaction between the catheter and the chest tube when bending exceeds a certain amount. Increasing contact points between the catheter and the chest tube can also lead to energy loss, which constrains the deflection to an even greater extent. Therefore, bending a catheter beyond a wire tension of 10 N is not only difficult to predict with the simulation, but also inefficient.
Parameters affecting target accessibility of catheter tip
The FGAP operation can be performed more effectively by selecting the best type of catheter and determining the optimum overhang and wire tension. Catheter selection and parameter decisions are made considering various deforming behaviors of different catheters and the location of the defect. Parameter selections are based on the parameters of the simulation generating the best accessibility indexes defined in the previous section.
Effect of segment stiffness on catheter deflection
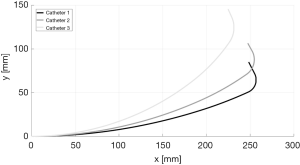
Simulation results with different catheters constrained by the chest tube are presented in Figure 9. Segment curvatures and tip slope information for a pull-wire tension of 10 N are summarized in Table 3. The tip slope in the table is the angle that the distal end makes relative to the angle at the end of the proximal shaft.
Full table
Catheter 3 has excessive deflection at the proximal shaft compared to the other two catheters due to its relatively small stiffness at the proximal shaft. Furthermore, catheter 3 has a relatively small deflection at the distal shaft because of its high stiffness. Although the distance between the chest tube and the surface of the lung can vary for different FGAP operations, the area in the chest cavity where catheters can deform is usually very narrow. Therefore, a large deflection of the proximal shaft reduces the area for the distal shaft to deform. Since distal shaft deformation is critical for a better angle index, a large deflection of the proximal shaft is undesirable. For this reason, catheter 3 is not effective for any kind of FGAP operation. Catheter 1 and catheter 2, on the other hand, can be desirable since they have a large range of tip slope. Catheter 1, with the smallest curvature at the proximal shaft and the biggest tip slope, is thus the most desirable.
Effect of overhang and pull-wire tension on catheter tip positioning
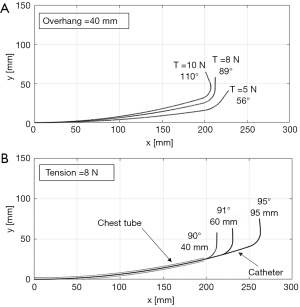
Figure 10 shows the simulated deflection curves of catheter 1 constrained by the chest tube as both the overhang and the tension is varied. Controlling the tip slope can be achieved more effectively through changing the wire tension rather than changing the overhang. Overhang control is useful for approaching the defect area. Specifically, a longer catheter overhang is superior for reaching defects in the apex, while a shorter overhang is better for defects in the lateral surface. Once the overhang is adjusted depending on the location of the lung defect, the tip slope can be optimally controlled by wire tension. During an actual operation, overhang can be controlled through linear motor and tension can be controlled by determining the handle knob rotation angle. Knob would be connected to a rotary motor in which the position control will be performed.
Evaluation of target accessibility of a catheter on a lung model
Two cases, shown in Figure 11, are explored to make optimal choices through simulation. The point of origin is positioned at the lower left-hand corner of the lung, as indicated in Figure 11. The defect coordinate is selected as (200 mm, 47 mm) for case 1 and (160 mm, 25 mm) for case 2. The slope of the tangent plane of the defect relative to the horizontal line is 36.8° and 36.7° for case 1 and 2, respectively. The tip of the chest tube is placed at (80 mm, 40 mm). A 40 mm distance from the surface of the lung to the chest tube is a reasonable distance for FGAP operations. Catheters 1 and 2 are considered for evaluating accessibility.
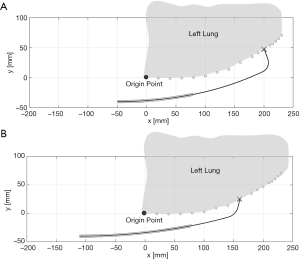
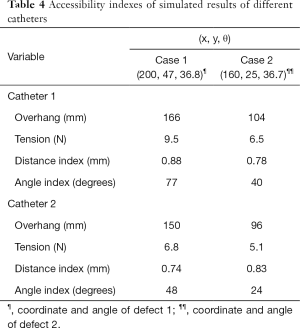
The required tension and overhang for each catheter is found by trial and error with simulation. The accessibility indexes for each catheter are determined, as shown in Table 4. Both catheters exhibit very good distance indexes; whereas, the angle index is generally poor. Catheter 1 is the best choice for both cases 1 and 2 concerning angle index. The angle index of catheter 1 is noticeably better than that of catheter 2.
Full table
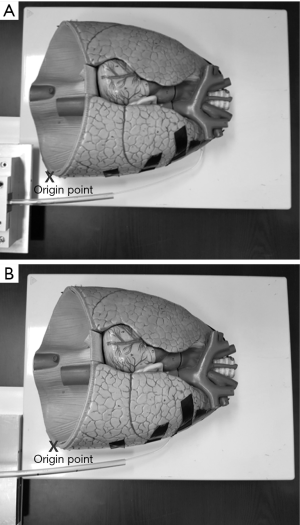
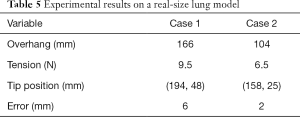
Figure 12 illustrates a test setup of a catheter inserted through a chest tube approaching different defect locations using a real-size human lung model. The relative catheter position between the catheter and the lung is set the same as the simulation environment. Catheter 1 is used for the experiment, and the corresponding tension and overhang found from the simulation are applied. The experimental results are compared in Table 5. The maximum distance error of the tip to the designated defect location occurring at case 1 is approximately 6 mm, which is acceptable for FGAP operations.
Full table
During the actual FGAP operations using the proposed method, the operator first determines the coordinate of the defective spot on a lung using X-rays. Then, the simulation tool is used prior to operation for selecting the best catheter type and determining the appropriate overhang and pull wire tension. After all the parameters have been defined through simulation, the surgery can be performed using the determined parameters improving the target accessibility of the tip.
Conclusions
Steerable catheters are currently regarded as an efficient tool for the intervention of sealant injection to air-leaked defects of lung. The main problem is controlling the position and slope of a catheter tip to the precise defect location. This paper proposes a method which can assist medical doctors to select a desirable catheter configuration, and even an optimal pull-wire tension and overhang length, for superior intervention using catheter deflection simulation software developed by the authors. The new findings are as follows:
- The optimal catheter configuration is selected depending on the location of the lung defects;
- The simplified simulation model can accurately reflect the deflection of a catheter constrained by a chest tube with an error of less than 5 mm;
- Excessive deflection at the proximal shaft reduces the accessibility of the tip to the defect by limiting the space for the distal shaft to deflect;
- Controlling the overhang and wire tension according to the simulation result enables effective target accessibility of the tip of the catheter.
Ultimately, overhang and tension control should be automated through use of motors. In the future, catheter handle capable of controlling overhang and tension through motors will be designed. Also, the relationship between the pull wire extension length and the tension will be investigated.
Acknowledgments
Funding: This work was supported by the Bio & Medical Technology Development Program of the National Research Foundation (NRF) funded by the Korean government (MSIT) (No. NRF-2018M3A9E8066255).
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This article does not involve any patients or animals, and the ethical review is exempted.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Paramasivam E, Bodenham A. Air leaks, pneumothorax, and chest drains. Contin Educ Anaesthesia Crit Care Pain 2008;8:204-9. [Crossref]
- Mo A, Luo Y, Yang X, et al. Low-cost biportal endoscopic surgery for primary spontaneous pneumothorax. J Thorac Dis 2015;7:704-10. [PubMed]
- Kurihara M, Kataoka H, Ishikawa A, et al. Latest treatments for spontaneous pneumothorax. Gen Thorac Cardiovasc Surg 2010;58:113-9. [Crossref] [PubMed]
- June M. Thoracographic fibrin glue sealing: a novel interventional treatment for pneumothorax with intractable persistent air leakage. Interact Cardiovasc Thorac Surg 2016;23:i38.
- Schlag G, Heidelberg B, York N, et al. editors. Fibrin Sealant in Operative Medicine. Springer-Verlag Berlin Heidelberg, 1986.
- Lee S, Park SY, Bae MK, et al. Efficacy of polyglycolic acid sheet after thoracoscopic bullectomy for spontaneous pneumothorax. Ann Thorac Surg 2013;95:1919-23. [Crossref] [PubMed]
- Ganji Y, Janabi-Sharifi F. Catheter Kinematics for Intracardiac Navigation. IEEE Trans Biomed Eng 2009;56:621-32. [Crossref] [PubMed]
- Khoshnam M, Patel R V. Tendon-sheath analysis for modeling and control of steerable ablation catheters. IEEE/ASME Int Conf Adv Intell Mechatronics AIM 2016;2016-Septe:1585-90.
- Ryu J, Ahn HY, Kim HY, et al. Analysis and simulation of large deflection of a multi-segmented catheter tube under wire tension. J Mech Sci Technol 2019;33:1305-10. [Crossref]
- Asai K, Urabe N. Secondary spontaneous pneumothorax associated with emphysema and ruptured bullae at the azygoesophageal recess. Gen Thorac Cardiovasc Surg 2008;56:539-43. [Crossref] [PubMed]
- Choi J, Ahn HY, Kim YD, et al. Location of ruptured bullae in secondary spontaneous pneumothorax. Korean J Thorac Cardiovasc Surg 2017;50:424-9. [Crossref] [PubMed]
- Lewis G, Monasa F. Large deflections of cantilever beams of nonlinear materials. Comput Struct 1981;14:357-60. [Crossref]