Hemodynamic evaluation and in vitro hemolysis evaluation of a novel centrifugal pump for extracorporeal membrane oxygenation
Introduction
Extracorporeal membrane oxygenation (ECMO) is a temporary mechanical circulatory system established outside the body to provide respiratory and hemodynamic support for patients with severe cardiopulmonary failure. A report from the Extracorporeal Life Support Organization found that the use of ECMO had risen exponentially in recent years [ELSO (2017)]. However, adverse events are still common in patients using ECMO. The major presentations are bleeding, thrombosis, and stroke (1-4). The centrifugal blood pump is an indispensable component of the ECMO system. It provides power for the circulation of blood outside the body, so the majority of blood damage occurs in the blood pump. All aspects of the blood pump must be evaluated before it enters clinical use.
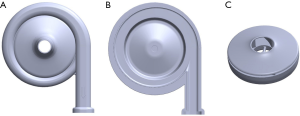
The STM CP-24 I ECMO centrifugal pump is a new centrifugal blood pump developed by Jiangsu STMed Technology Co. Ltd. (Jiangsu, China) for the OASSIST® ECMO system of the Jiangsu STMed Technology Co. Ltd. (Figure 1). This system contains a separate control console and a separate centrifugal pump driver, which can work independently to facilitate patient transfer and later activities. The control console integrates the functions of sensing and processing the temperature, pressure, and flow signals and can record relevant parameters during operation in real time. However, in the OASSIST® ECMO system, the hemodynamic characteristics and blood compatibility of the STM CP-24 I centrifugal pump are still unclear. This study combined computational fluid dynamics (CFD) analysis and in vitro experiments to analyze and evaluate them.

At present, the application of CFD for hemodynamic analyses of blood pumps is considered an important method for evaluating the blood compatibility of blood pumps before clinical use (5). CFD can accurately simulate the flow inside a blood pump and reduce the costs of the development and laboratory testing of blood pumps. In 2016, the U.S. Food and Drug Administration approved the use of CFD in the field of medical device evaluation, reflecting the importance of this method (6). Bozzi et al. used the CFD method to study the blood compatibility of a centrifugal pump with two impeller designs. They analyzed the pressure distribution and velocity vector distribution in the centrifugal pump and predicted platelet activation due to abnormal shear stress histories (7). Tompkins et al. designed a magnetically levitated rotary blood pump for pediatric use. They used the CFD method to optimize the fluid structure and calculated and analyzed the pump’s hydraulic performance (8). Thamsen et al. combined the CFD method with particle image velocimetry to study the flow field of the HeartMate 3 (9). Chang et al. used CFD to study the mechanical and hemolytic performance of four different commercial centrifugal pumps (10).
The in vitro hemolysis experiment is an important way to evaluate the blood compatibility of blood pumps. Its purpose is to evaluate the degree of blood damage caused by mass-produced blood pumps in practical use. The normalized index of hemolysis (NIH) is a quantitative indicator of the hemolytic performance of a blood pump. In other words, the degree of destruction of red blood cells caused by blood pumps is quantitatively analyzed and evaluated using standardized experimental procedures and measurement steps. It is generally considered that a value of NIH larger than 0.1 g/100 L indicates hemolysis in the blood pump. The American Society for Testing and Materials standard F1841-97 provided specific guidance for testing the hemolysis of continuous-flow blood pumps (11). Under the given working conditions, blood pumps are continuously tested for 6 hours, and samples are collected once every hour to measure the level of free hemoglobin in blood samples, to finally obtain the NIH value of the tested blood pumps. Chan et al. performed in vitro hemolysis experiments on the CentriMag® centrifugal blood pump and obtained its NIH values (12). Zhang et al. used in vitro hemolysis experiments and CFD-based calculation and analytical methods to study the NIH of the CentriMag® (13).
This study used hydraulic experiments, CFD calculation and analysis, and in vitro hemolysis experiments to analyze the performance of the STM CP-24 I ECMO centrifugal pump. The flow field distribution, pressure distribution, and speed inside the blood pump were obtained through CFD calculation to measure its hemodynamic performance. Fresh blood samples from healthy goats were collected for in vitro hemolysis experiments (n=3) to obtain the NIH value of the blood pump.
We present the following article in accordance with the MDAR reporting checklist (available at http://dx.doi.org/10.21037/atm-21-1135).
Methods
Centrifugal pump
The STM CP-24 I ECMO centrifugal pump was from Jiangsu STMed Technology Co. Ltd. (Jiangsu, China), precharge volume is 24 ml which less than others. Its structure is shown in Figure 2. It was composed of (A) the upper case of the volute, (B) the lower case of the volute, and (C) the rotor blade with a shroud. The priming volume of the centrifugal pump was 24 mL. The inlet and outlet both used the 3/8″ standard pipe diameter. The blade was designed with a shroud, and the rotation of the rotor was driven by magnetic coupling. The centrifugal pump had a rated rotating speed of 1,000–5,500 rpm, a maximum rated head pressure of 500 mmHg, and a designed flow of 0–8 L/min.
Hydraulic experiment
The pressure-flow curve of the centrifugal pump was drawn using hydraulic experiments. On one hand, whether the centrifugal pump could meet the flow and pressure required for clinical use was confirmed; on the other hand, the results provided a reference for the calculation of grid independence using CFD (7). The working ranges of the pump measured in hydraulic experiments were a rotating speed of 1,000–5,500 rpm, with an interval between measurement points of 500 rpm, and a flow of 0–8.0 L/min, with an interval between measurement points of 0.5 L/min
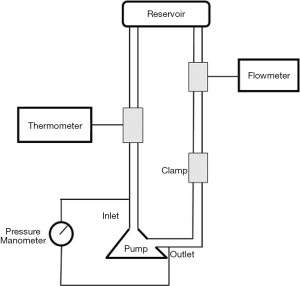
To maintain consistency in the blood compatibility results, the circulation platform was established according to the standard for hemolysis experiments. The test loop is shown in Figure 3. The loop that was consistent with our in vitro hemolysis experiments was used for measurement. The test loop included one polyvinyl chloride pipe with a total length of 2 m and an inner diameter of 9.5 mm. The reservoir was a modified standard blood bag. The outlet and inlet of the blood pump each had a manometer. The damping valve was downstream of the manometer at the outlet of the blood pump. The flow meter was upstream of the inlet of the blood pump. The test medium was the simulated blood containing a mixture of 0.9% NaCl solution (Beijing Salt Industry Corporation of China National Salt Industry Corporation, China) and glycerin (Tianjin Zhiyuan Chemical reagents Co. Ltd., China) at the ratio of 2.3:1.
Geometric model and grids
As shown in Figure 4, the structural model of the blood pump was filled to obtain the fluid model of the blood pump, and the outlet position of the blood pump was appropriately extended. Based on our calculation needs, the fluid part of the blood pump was divided into three parts: the static zones near the inlet and outlet and the rotation zone where the blade was.
Tetrahedral grids were used to discretize the computational region, and six boundary layers were added at the fluid-solid interface. Higher grid densities were used near the blade to obtain accurate local velocity gradients. The grid size was determined after conducting pilot convergence studies in order to ensure the correct grid independence. More specifically, three different numbers of grids (2, 4, and 8 million grid units) were used under the same simulation conditions for calculation, and their calculated head pressures were 289, 310, and 310 mmHg, respectively. In contrast, the experimental value of head pressure was 317 mmHg. Because the flow fields in the blade gap and near the wall had the greatest impact on the hemolytic performance of the blood pump, the setting of 8 million grids was selected for further analysis. Finally, 8,054,711 grid units were delineated; the unit size was 200 µm close to the blade and 400 µm in other areas.
Hemodynamic calculation
The hydrodynamic calculation is a steady-state calculation. Blood is considered an incompressible Newtonian fluid. The flow of blood satisfies the conservation of mass, momentum, and energy and can be obtained by solving the Navier-Stokes equation of three-dimensional incompressible flow. The calculation assumed that blood was a Newtonian fluid with a density of 1,050 kg/m3 and a dynamic viscosity of 0.0035 Pa·s (14). Fluent2019 was the solver used for the numerical simulation, the speed-pressure coupling used the SIMPLEC algorithm, and turbulence and momentum were solved using the second-order upwind scheme to ensure calculation accuracy (7). The residuals of the dynamic momentum equation of the continuity equation adopted 10−4 as the convergence criterion. The boundary conditions of zero pressure at the inlet and zero mass flow at the outlet were set. The rigid-body rotation of the rotor blade was realized using the frame motion method.
The three-dimensional shear stress tensor was derived from the velocity field obtained from the numerical simulation of blood flow. The scalar shear stress force calculation formula was as follows Eq. [1]:
In the shear stress calculation, addition of the Reynolds stress tensor would result in shear fields with higher calculated numerical values. Reynolds shear stress is a statistical value that does not have a direct relationship with the physical force. Therefore, the shear stress component in Eq. [1] only considered the viscous stress tensor (15).
The calculation simulated the upper limit of the working conditions of the centrifugal pump that are commonly used in the clinic, which were 4,000 rpm and 5 L/min. Under these conditions, the measured head pressure was 317 mmHg, and the calculated head pressure was 310 mmHg (7).
In vitro hemolysis experiment
Blood for testing
Blood for testing (Nong Nong (Beijing) Biotechnology Co., Ltd., China) was collected in a standard blood storage bag (Suzhou Laishi Transfusion Equipment, China) containing the blood preservation solution CP2DA (14 mL preservation solution in every 100 mL blood). During collection, blood flowed out naturally by gravity. The blood samples were used within 6 hours of collection. Before testing, the hematocrit was adjusted to 30%±2%, and the content of free hemoglobin was ensured to be lower than 2 mg/dL (ensuring that red blood cells were not destroyed during the collection process). The blood was heated to physiological temperature in a 37±1 °C water bath before use.
Device operation and specifications
As shown in Figure 3, the test loop included one polyvinyl chloride pipe with a total length of 2 m and an inner diameter of 9.5 mm. The reservoir was a modified standard blood bag (Suzhou Laishi Blood Transfusion Equipment). One manometer was at the outlet and one at the inlet of the blood pump. The damping valve was downstream of the manometer at the outlet of the blood pump. The flow meter was upstream of the inlet of the blood pump. According to the testing requirements of the China Food and Drug Administration, during the hemolysis experiment the flow of the blood pump was 8±0.25 L/min, the circulating blood temperature was 37±1 °C, the inlet and outlet pressure difference was 300±5 mmHg, and the volume of circulating blood in the whole loop was 500±5 mL. The ambient temperature of the system was kept above 30 °C to minimize the temperature gradient in the pipeline. The reservoir was 60–80 cm higher than the blood pump level to ensure the negative pressure near the inlet of the blood pump was not too low during the test, thus avoiding the influence of too low negative pressure on the accuracy of test results.
Experimental procedure
The whole test loop was immersed in phosphate-buffered solution (Haibiao Science and Technology, Xiamen, China) before the experiment, and the blood pump was first operated for 20 minutes under a low speed to fully immerse the blood contact surface. Next, the buffer solution in the test loop was emptied. Blood was slowly heated to 37 °C and added into the test loop through a three-way valve by gravity, and bubbles were emptied from the loop. The rotation speed of the blood pump and the damping valve were adjusted to the experimental conditions to be measured. After the blood pump operated for approximately 5 minutes under the test condition and bubbles had been emptied from the loop, the first blood sample was collected through the sampling port on the blood bag, becoming the blood sample at time 0.
The whole testing period was 6 hours. After the first blood sample was collected, the sample was collected once every hour for a total of seven blood samples. To ensure the accuracy of sampling in the experiment, 2 mL blood was removed from around the collection port to exclude blood samples that might contain blood trapped near the sampling port. Next, 1.5 mL of the collected blood was placed in a centrifuge tube and centrifuged at 3,000 rpm for 8 minutes (D2012 plus, Beijing DLAB Scientific, China), and the supernatant was collected for measurement of free hemoglobin in plasma.
Measurement of free hemoglobin
The ferrous ion (Fe2+) in the hemoglobin molecule is oxidized by potassium ferricyanide into the ferric ion (Fe3+) in the van Kampen-Zijlstra’s reagent (Zhongshan Research Institute, Tianjin Modern High Technology Co., Ltd., China) to form methemoglobin (Hi). It later reacts with cyanide ion (CN−) to generate cyanmethemoglobin (HiCN). HiCN has a maximum absorption peak at 540 nm, and the absorbance of HiCN at 540 nm is proportional to the concentration of HiCN. Therefore, the hemoglobin concentration can be calculated from the absorbance measured by a spectrophotometer as shown in Eq. [2]:
where c is the hemoglobin concentration (g/L); is the absorbance of the HiCN solution at 540 nm; 16,114.5 is the relative molecular weight of a hemoglobin monomer (the relative molecular weight of hemoglobin composed of four monomers is 64,458); F is the dilution of the test sample; 11.0 is one-fourth of the millimolar extinction coefficient of the HiCN solution at 540 nm; d is the optical length of the spectrophotometer and is 1.000 cm; and 1,000 in the denominator is the multiplicator to convert milligrams to grams.
Hemolysis measurement and statistical analysis
The formula for calculation of NIH is shown in Eq. [3]:
where:
- NIH is the normalized index of hemolysis (g/100 L);
- ∆free Hb is the increment of free hemoglobin in plasma within the sampling interval (g/L);
- V is the volume of blood in the test circulation loop (L);
- Q is the flow speed (L/min);
- Hct is the hematocrit (%); and
- T is the sampling interval (min).
The results of each single experiment remain four decimal places. And mean values and standard deviations were calculated for all experimental results, which remain four decimal places.
Results
Hydraulic characteristics
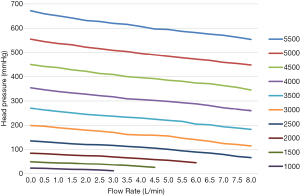
Figure 5 shows the head pressure-flow curve of the blood pump after the actual measurement. Under the same flow conditions, the head pressure increased linearly with the rotation speed. At the same rotation speed, the head pressure decreased linearly with the increase in flow. At the same rotation speed, there was an approximately linear relationship between the head pressure and flow, and there was no distortion point in the whole working range, indicating that the pump worked well over that range. In addition, this linear relationship can ensure its safety in clinical use. When doctors adjust the working conditions, they will have a reasonable expectation that the pump will not have an abnormal working condition. Furthermore, head pressure with a maximum rotation speed of 5,500 rpm, a maximum flow of 8.0 L/min, and a maximum head pressure of 550 mmHg can meet clinical needs.
Pressure distribution
Figure 6 shows the static pressure distribution in two sections (the longitudinal section along the midline of the pump inlet and the horizontal section along the middle of the pump blade) and on the surface of the volute and rotor at a rotation speed of 4,000 rpm and a flow of 5 L/min. As expected, due to the rotational movement of the rotor blades, blood was pushed to produce a head pressure. Blood entered the pump at a lower pressure and flowed out of the pump at a higher pressure. Figure 6 shows the evenly distributed pressure field. Figure 6A,B show that due to the suction caused by centrifugal motion, a low-pressure zone occurred at the opening position of the impeller center, resulting in a low pressure on the inner surface of the impeller/rotor, as shown in Figure 6D). However, the pressure at the outer end of the blade (blade tip) was relatively high.
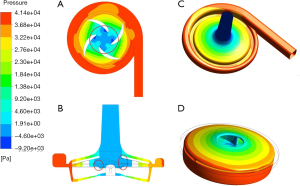
Flow field distribution
Figure 7 shows the flow characteristics of the section along the midline of the pump inlet and the horizontal section in the middle of the blade. Blood entered the pump from the inlet at a lower speed and was accelerated in the rotor area. The blood flow slowed down after the blood entered the volute area. Blood then flowed out from the outlet of the pump along the volute. There were two backflow paths between the rotor blade and the volute, as shown by the dotted line in Figure 7A).
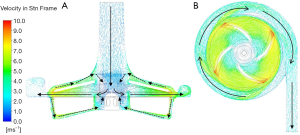
The more detailed three-dimensional CFD results are shown in Figure 8. There was a more complex flow structure near the central section (Figure 8B). Careful observation showed that there was a turbulence zone in the lower part of the rotor center. This was because the blood flow at the axial position of the flow path was slower than that accelerated by rotational motion. The inner blood flow preferentially entered the rotor blades. This part of the flow moved downward and connected to the backflow paths; finally, it moved upward into the blades. This flow could help to produce better surface cleaning inside the rotor.
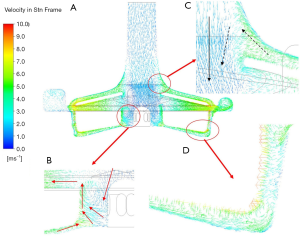
Because there was a backflow path between the upper case and the outer case of the impeller (Figure 8C), the accelerated blood flowed in the opposite direction along a path close to the wall of the inlet pipe. At this time, when the momentum of the counterflow blood was too low to drive the blood flow against the main flow at the inlet, the blood flow re-entered the main flow and continued to flow without affecting the main flow in the blood pump. The other backflow path was between the bottom of the rotor and the outer case (Figure 8D). Further observation of the enlarged figure of the indicated gap zone showed that, although the flow in this zone was very unstable under the influence of the rotor, the overall flow was downward, indicating that the final evolutional trend of turbulence was to flow to the bottom of the rotor and to continue to flow to the supporting point of the rotor center.
Shear stress distribution
Shear stress is considered one of the major factors causing hemolysis. Many researchers have used shear stress distribution to explain the hemolytic performance of blood-contacting devices (8,13). Eq. [1] was used to calculate the scalar shear stress distribution. Figure 9 shows the distribution of areas inside the pump with shear stress >150 Pa. The maximum stress occurred in the local area of the upper corner of the rotor section and the blade/rotor connection. At this time, the rotation speed of the pump was 4,000 rpm, the flow was 5 L/min, and the head pressure was 310 mmHg.
NIH
Figure 10 shows two cases from the three hemolysis experiments. Hemolysis experiments were performed when the centrifugal pump was operated at 4,098 rpm, 8 L/min, and 300 mmHg of the head pressure. After collection of blood (Nong Nong (Beijing) Biotechnology Co., Ltd., China), the adjusted hematocrit was 29%, and the ambient temperature was 36±1 °C. The temperature of the circulating blood was controlled using a temperature-control water bag during experiments to keep the temperature at 37±1 °C. Experiments were performed 4 hours after blood collection and lasted for a total of 6 hours.
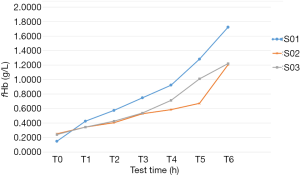
Figure 11 shows the curve of the change in free hemoglobin in the blood samples over time in the in vitro hemolysis experiments. In the S01 experiment, due to the inevitable damage to the red blood cells during the blood drawing and priming process, some red blood cells were more prone to hemolysis under the action of shear stress. Therefore, the increment of free hemoglobin at hour 1 was higher than those at hours 2 and 3. At hours 5 and 6, the increment of free hemoglobin was higher than those at the other hours, perhaps because although the red blood cells were damaged by the shear stress to a certain extent during the first 4 hours of the circulation, these injuries did not cause their disruption. With the continuous accumulation of this type of damage, a threshold of red blood cell disruption will eventually be reached; therefore, the increment of free hemoglobin in the final 2 hours significantly increased.
In the S02 and S03 experiments, the increments of free hemoglobin in the first 3 hours were similar. However, at hours 4 and 5, the increments of hemoglobin were stable in the S02 experiment and significantly increased in the S03 experiment. At hour 6, the increment of free hemoglobin in S02 significantly increased. The cause of this phenomenon can be the above-mentioned damage accumulation.
Finally, the above experimental data were processed. Eq. [3] was used to calculate the NIH values corresponding to the three different experiments (Table 1). The mean NIH value of the STM CP-24 I ECMO centrifugal pump obtained from the in vitro hemolysis experiment was 0.0125± 0.0022 g/100 L.

Full table
Discussion
Hydraulics experiments were performed on the STM CP-24 ECMO centrifugal pump to plot the pressure-flow curve. The results showed that pressure changed linearly with flow in the centrifugal pump over the whole working process, which indicated that the flow field design of this pump was reasonable and that there was no pressure distortion in the working process that would bring risks in clinical use. In addition, the pressure-flow curve showed that the pump in the working period will satisfy clinical needs.
In the CFD calculation and analysis, grid partitioning in the model used the unstructured tetrahedron and semistructured mixed model for investigation. Grid independence analysis was used to calculate changes in the head pressure of the pump in different grid partitions. Finally, considering the analysis of the details of the structure and the closest approximation to the measured head pressure, approximately 8 million grid units were selected for CFD calculation and analysis. The turbulence model used the k-ω shear stress transport model, and the calculation results showed that the simulated head pressure was in good agreement with the measured head pressure.
As shown by our analysis of the pressure field and velocity vector in the blood pump, the flow in the main flow path was a streamline type, the rotor surface was well washed, and the low-speed zone in the center of the blade had better influx. These results indicate that the flow field design was successful. However, backflow paths and several flow circulations were observed at different locations in the apparatus. These flows effectively washed the bottom surface and sidewalls of the volute and promoted blood flow in low-speed zones near the support point of the rotor, thus effectively reducing the risk of thrombosis.
Furthermore, the three-dimensional scalar shear stress tensor obtained from our velocity field calculations indicated that there was no abnormally increased shear stress near the blade and that the area in the blood pump with shear stress larger than 150 Pa accounted for less than 1% of the total area. Although there was some high shear stress in the gap between the rotor blade and the volute, the flow at that location was not the main flow, its area was small, and its effect on overall hemolysis was limited. The results of the in vitro hemolysis experiment could explain this phenomenon.
The in vitro hemolysis experimental results yielded the mean NIH value of 0.0125±0.0022 g/100 L for the centrifugal pump, which was within the clinical limit range, indicating that the centrifugal pump had high blood compatibility and that the design was successful. Compared with two ECMO centrifugal pumps currently in clinical use, the RotaFlow had a NIH (0.021±0.0022 g/100 L) and the CentriMag had a NIH (0.041±0.0010 g/100 L), which were worked in 4.20±0.3 L/min and 250±10 mmHg for head pressure, the STM CP-24 centrifugal pump had a lower NIH (16). In addition, during testing in the in vitro hemolysis experiment, the centrifugal pump was operated at the rotation speed of 4,098 rpm, the flow of 8 L/min, and the head pressure of 300 mmHg, which were much higher than the commonly used clinical values and led to more severe destruction to red blood cells. Therefore, there is reason to believe that the destruction of red blood cells by the pump will be less severe during clinical use.
Conclusions
In summary, the STM CP-24 I ECMO centrifugal pump has an improved flow field design, and in vitro hemolysis experiments showed high blood compatibility. Research at the next stage should mainly investigate and verify other aspects of this pumps using thrombosis experiments, fatigue and endurance tests, preclinical animal experiments, and clinical experiments in order to prepare the pump for clinical use, strive for early clinical use, and save more patients with severe symptoms.
Acknowledgments
Funding: This study was partly funded by the National Natural Science Foundation of China (Grant Nos. 61931013, 81701644 and 11832003), the Key Research and Development Program (2017YFC0111104), the Key Research and Development Program of Shanxi Province (201903D321149), the Key Research and Development Program of Wuhan province (WX18A01), and the New Talent (015000514118002) and Youth Top Talent Training Programs (CIT&TCD201904025).
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at http://dx.doi.org/10.21037/atm-21-1135
Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-21-1135
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-21-1135). Dr. Wang reports support from Jiangsu STMed Technology Co. Ltd. (Suzhou, China), which provides the STM CP-24 centrifugal pump for experiment. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Badheka A, Stucker SE, Turek JW, et al. Efficacy of Flow Monitoring During ECMO. ASAIO J 2017;63:496-500. [Crossref] [PubMed]
- Appelt H, Philipp A, Mueller T, et al. Factors associated with hemolysis during extracorporeal membrane oxygenation (ECMO)-Comparison of VA- versus VV ECMO. PLoS One 2020;15:e0227793 [Crossref] [PubMed]
- Garg M. Intravascular Hemolysis and Complications During Extracorporeal Membrane Oxygenation. Neoreviews 2020;21:e728-40. [Crossref] [PubMed]
- Besser MW. Post-operative of bleeding, haemolysis and coagulation in mechanical circulatory support patients. Ann Transl Med 2020;8:832. [Crossref] [PubMed]
- Fraser KH, Taskin ME, Griffith BP, et al. The use of computational fluid dynamics in the development of ventricular assist devices. Med Eng Phys 2011;33:263-80. [Crossref] [PubMed]
- Heck ML, Yen A, Snyder TA, et al. Flow-Field Simulations and Hemolysis Estimates for the Food and Drug Administration Critical Path Initiative Centrifugal Blood Pump. Artif Organs 2017;41:E129-40. [Crossref] [PubMed]
- Bozzi S, Vesentini S, Santus M, et al. Fluid dynamics characterization and thrombogenicity assessment of a levitating centrifugal pump with different impeller designs. Med Eng Phys 2020;83:26-33. [Crossref] [PubMed]
- Tompkins LH, Gellman BN, Morello GF, et al. Design and Computational Evaluation of a Pediatric MagLev Rotary Blood Pump. ASAIO J 2020; Epub ahead of print. [Crossref] [PubMed]
- Thamsen B, Gulan U, Wiegmann L, et al. Assessment of the Flow Field in the HeartMate 3 Using Three-Dimensional Particle Tracking Velocimetry and Comparison to Computational Fluid Dynamics. ASAIO J 2020;66:173-82. [Crossref] [PubMed]
- Chang M, Hur N, Moshfeghi M, et al., editors. A Numerical Study on Mechanical Performance and Hemolysis for Different Types of Centrifugal Blood Pumps. ASME 2015 International Mechanical Engineering Congress and Exposition; 2015.
- ASTM F1830-97(R 2017).pdf. Available online: https://www.astm.org/DATABASE.CART/HISTORICAL/F1841-97R05.htm
- Chan CH, Pieper IL, Hambly R, et al. The CentriMag centrifugal blood pump as a benchmark for in vitro testing of hemocompatibility in implantable ventricular assist devices. Artif Organs 2015;39:93-101. [Crossref] [PubMed]
- Zhang J, Gellman B, Koert A, et al. Computational and experimental evaluation of the fluid dynamics and hemocompatibility of the CentriMag blood pump. Artif Organs 2006;30:168-77. [Crossref] [PubMed]
- Girdhar G, Xenos M, Alemu Y, et al. Device thrombogenicity emulation: a novel method for optimizing mechanical circulatory support device thromboresistance. PLoS One 2012;7:e32463 [Crossref] [PubMed]
- Bludszuweit C. Model for a General Mechanical Blood Damage Prediction. Artificial Organs 1995;19:583-9. [Crossref] [PubMed]
- Sobieski MA, Giridharan GA, Ising M, et al. Blood trauma testing of CentriMag and RotaFlow centrifugal flow devices: a pilot study. Artif Organs 2012;36:677-82. [Crossref] [PubMed]