
Predicting the cumulative number of disaster deaths during the early stage of earthquakes
Introduction
Although the land area of Japan accounts for only 0.3% of the entire world, more than 20% of earthquakes with a magnitude of 6 or greater on the moment magnitude scale occur in Japan (1). Japan accounts for 11.9% (1) of the total economic impact caused by natural disasters across the world, which indicates that the frequency of natural disasters in Japan is very high. The number of disaster deaths in Japan that were caused by earthquakes has been far greater than the numbers of deaths caused by other natural disasters in the last 50 years (e.g., about 90% of total deaths in the last three decades were caused by earthquakes) (2).
Natural disasters occur suddenly, immediately elevating various types of demand, and medical and public health responses should thus be implemented swiftly (3-5), particularly because the largest demand for medical treatment occurs during the first 24–48 hours (6). In principle, these responses are classified into three phases: (I) immediate; (II) early; and (III) delayed, and the treatment of injury during the early stage is known to contribute to reducing the cumulative risk of death (7).
In the event of a disaster, various medical teams are deployed in contexts around the world (8). In Japan, the Disaster Medical Assistance Team (J-DMAT) training program has been coordinated by the Ministry of Health, Labour and Welfare since 2005 (9). As a group of experts, a trained, mobile, self-contained medical team is organized to provide medical treatment in the acute phase in the devastated area (10). The team is rapidly deployed to any area of the country hit by a disaster, but the overall size and content of the team is not necessarily determined objectively and quantitatively. Although understanding the expected total number of deaths would help to coordinate this rapid deployment and contribute to minimizing damage, a simple prediction method has not yet been established. It is frequently the case that available datasets are restricted to time-dependent updates of fatalities, and using a prediction method that requires only these data could shed light on an earthquake’s overall anticipated death toll. Determining the size of the team to be deployed requires the quantitative measurement of the size of the disaster (e.g., the anticipated number of disaster deaths) (11). If the number of direct deaths could be predicted, an appropriate number of J-DMAT team members could be deployed, and the number of indirect deaths could be minimized.
Multiple forecasting studies on natural disasters have been conducted, but the majority of these studies have focused on forecasting the physical aspects of disasters (e.g., the extent of landslides) (12,13), anticipating the overall economic damage (14), or conducting an anatomical analysis of corpses to understand the nature of disaster deaths from the viewpoint of forensic medicine (15,16). A more direct exploration, using the number of deaths to predict the likely total death toll, is required. In the present study, we aimed to devise a simple method to predict the cumulative number of deaths during the early stage of a large earthquake using data that are readily available in official government reports. To accomplish this task using the minimal amount of available data, we examined the time trend of deaths during six large earthquakes in Japan. We present the following article in accordance with the MDAR reporting checklist (available at http://dx.doi.org/10.21037/atm-20-5784).
Methods
Earthquake data in Japan
Globally, the strength of an earthquake is measured using the magnitude, which is scaled by a seismic wave (17); however, Japan, where there are frequent earthquakes, has adopted the “shindo”, which measures seismic intensity (18). Shindo scales ground surface shaking, measured by the Japan Meteorological Agency, which has installed digital seismometers across Japan and directly performs measurements at 4,400 geographic observation points. The shindo scale ranges from 0 to 7. Shindo values of 6–, 6+, and 7 are defined as “difficult to remain standing”, “impossible to stand/cannot move without crawling” and “thrown off by the shaking and impossible to move at will”, respectively (18,19). In the present study, we focused on time series data obtained from death certificates issued during earthquakes with a moment magnitude (Mw) of 6.5 or greater (comparable to shindo 6+ or 7) from 1990 to 2018 that involved at least 20 deaths. Twenty deaths were selected because the decision to deploy J-DMAT has conventionally been determined by whether at least 20 people have been seriously injured in a disaster.
Specifically, we focused on direct deaths, which are defined as fatalities caused by the direct physical impact of the earthquake, including a collapsed building, fire, or tsunami. In Japan, during a natural disaster, all corpses undergo a postmortem examination, the police department provides updates on the cumulative number of deaths following these examinations, and press releases containing this information are published in newspapers or broadcast on television or the radio. In this study, we extracted the updated death certificate count from newspapers by searching Nikkei Telecom 21 (20), which is the largest business information service in Japan, including the full text of major Japanese newspapers for the past 30 years, using the search terms “earthquake” plus “death” or “earthquake” plus “fatality”. Our data were directly retrieved from the public news produced from police department reports, which can be regarded as the only official source of information on the time-dependent number of deaths. Because there was no concept of direct and indirect deaths in the 1990s, we simply counted the total number of deaths during earthquakes in that period; otherwise, we retrieved only direct death counts. Direct deaths were defined as death events for which the earthquake had a clear causal impact, whereas indirect deaths encompassed fatalities occurring during the evacuation process or the post-earthquake period that could be interpreted as induced by the earthquake. If the press release was made in the morning (before noon), the first decimal place of the corresponding time was set to 0; if the press release was made in the evening (after noon), this was set to 5.
Statistical analysis
First, we characterized the descriptive statistics, particularly with respect to the cumulative number of deaths during the selected earthquakes. The number of days from the mainshock that it took to reach a specific percentile point of deaths (e.g., median and first and third quartiles) was calculated and compared across different earthquakes. During the Kumamoto earthquake, an initial minor shock was followed by the mainshock. For this earthquake only, the time is measured from the first minor shock.
Second, parametric models with a monotonically increasing function of time since the mainshock were fitted in real time to the observed number of deaths over time. Two models with a small number of parameters, the exponential and Weibull distributions, were used because the exponential model requires only two parameters (i.e., the rate of increase and the predicted cumulative number of deaths) and the Weibull model can achieve a sigmoidal cumulative curve, i.e., the curve that captures the cumulative death pattern, better than the exponential distribution. Let the growth rate and the cumulative number of deaths be r and N, respectively. Using the exponential model, the expected number of deaths on day t since the mainshock was modeled as:
[1]
Similarly, let k be the shape parameter of the Weibull distribution. The expected number of deaths on day t since the mainshock was modeled as:
[2]
In addition, we explored the logistic model as an alternative approach:
[3]
Assuming that the observed number of deaths on day t since the mainshock followed a Poisson distribution, the maximum likelihood method was applied using Eq. [1], Eq. [2], and Eq. [3] as the expected value of the Poisson distribution and updating parameter estimates as time t progresses.
[4]
Where kt represents the observed death count at time t. The 95% confidence intervals (CIs) of the parameters were derived from the profile likelihood.
Third, as an alternative and more simply implemented method, we examined the prediction using the percentile point only (hereafter referred to as the percentile-based method). Let the observed q-th percentile point of the cumulative number of deaths be Mq. Using the single percentile point only, the expected total number of deaths E(N) is:
[5]
Specifically, we could use the median and first and third quartiles, that is, q =25, 50, and 75, to estimate the expected total number of deaths on a given date. However, in practice, we do not yet know that a certain number of days from the mainshock corresponds to the date on which the number of deaths reaches a percentile point. Thus, we explored the median number of days to reach q =25, 50, and 75 in our descriptive analysis and used the nearest integer value to define the date on which the q-th percentile was reached. This method remains as simple as Eq. [5]; however, an important drawback is that it does not include an uncertainty bound (e.g., 95% CI).
As an alternative method using a variety of datasets including detailed seismic and geographic information, the Prompt Assessment of Global Earthquakes for Response (PAGER) was used to offer another forecast of the earthquakes’ impact. The data required for PAGER were available only beginning in 2010; therefore, PAGER forecasting could be applied only to the Kumamoto and Hokkaido Eastern Iburi earthquakes.
Regarding the forecasts from the two parametric models, we assessed the validity and reliability of the abovementioned prediction methods at the immediate and early stages, that is, on days 3 to 6 since the mainshock. These days were selected because, at minimum, we needed 3 days to estimate the three unknown parameters of the Weibull distribution (because the degree of freedom, determined by the number of unknown parameters, required 3 days). Let
[6]
This is, in principle, using a chi-square test at the future time point to assess how expectations compare with the actual observed data.
More accurate real-time forecasts correspond to smaller values of (6). Reliability was assessed by the width of uncertainty, with the scale was adjusted by the observed number of deaths,
The validity of the percentile-based method was assessed in a similar manner to that used for the exponential and Weibull models. However, because there is no uncertainty bound for the percentile-based method, we could not assess its reliability. To compare model performance, the validity of the parametric models at the minimum number of days from the mainshock and that of the percentile-based method at the median point were overlaid for illustration.
Data sharing policy
In this study, we extracted the updated death certificate count from newspapers by searching Nikkei Telecom 21 (20). The original data used in this study are available as an online supplementary file (Table S1).
Results
There were 13 earthquakes with shindo 6+ or greater from 1990 to 2018. Of these, six earthquakes involved 20 or more deaths (Table 1), and the time-dependent updates of the death counts for these six earthquakes were used in the following analysis. Figure 1 shows the time series of the cumulative number of deaths as a function of time since the mainshock. There was a small number of considerably delayed corpse identifications following a landslide and tsunami; thus, there were some gaps in the increment of death. A corpse recovered on the shore and identified in later days is considered a lost person and designated as a direct death. Although the cumulative number of deaths differed markedly by earthquake, all distributions formed a cumulative curve that could be described by a sigmoidal function.

Full table
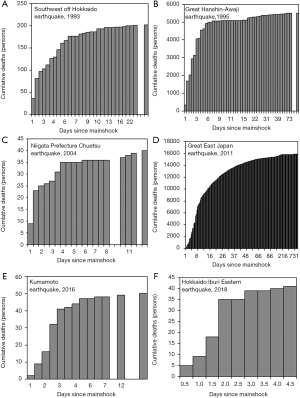
The time to reach the median and first and third quartiles of the cumulative number of deaths for the six selected earthquakes is shown in Figure 2. The median estimates for the lower quartile, median, and upper quartile were 1.5, 2.2, and 3.8 days, respectively. Among the six selected earthquakes, the Great East Japan earthquake in 2011 tended to be an outlier in the distributions, and only this earthquake involved a large number of fatalities because of the of vast land area affected as a result of a tsunami, whereas other earthquakes were epicentral or affected a restricted geographic area. Excluding the 2011 Great East Japan earthquake, the median estimates for the lower quartile, median, and upper quartile were 1.5, 2.0, and 3.5 days, respectively.

Figure 3 shows a comparison of the observed and predicted cumulative number of deaths using the exponential and Weibull distributions on day 4 since the mainshock. Before day 4, forecasts using the Weibull distribution did not converge and, on day 3, forecasts using the exponential model did not consistently converge for all earthquakes. Qualitatively, it was difficult to judge whether an inflection point had been reached; thus, the model did not smoothly converge on or before day 3. Except for the Southwest-off Hokkaido earthquake, forecasts made with the exponential model tended to overestimate the cumulative number of deaths. Visually, the Weibull model aligned well with the data for the Great Hanshin-Awaji, Kumamoto, and Hokkaido Eastern Iburi earthquakes. The logistic model did not converge for half of the earthquakes on day 4, and the fit was worse compared with exponential and Weibull models. The logistic model was thus discarded in the following analyses.
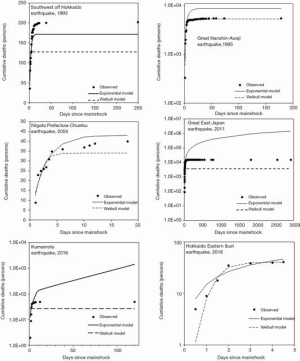
Figure 4 shows an evaluation of the validity and reliability of the forecasts from day 3 to 6 since the mainshock. The Southwest-off Hokkaido and Niigata Prefecture Chuetsu earthquakes were relatively well forecasted using both the exponential model and the Weibull model. In contrast, the Great East Japan earthquake yielded the greatest error for both models (Figure 4A,C), which indicates the difficulty of forecasting death during a very large-scale earthquake. The error, a measure analogous to chi-square, generally decreased as a function of time since the mainshock; however, the reliability did not necessarily demonstrate a decreasing trend over time. No consistent pattern of reliability was identified for the earthquakes using the exponential or Weibull model. The Great East Japan earthquake was difficult to predict, and there was not necessarily improvement over time in the prediction’s validity or reliability. Results from percentile-based method are shown as the online supporting material.
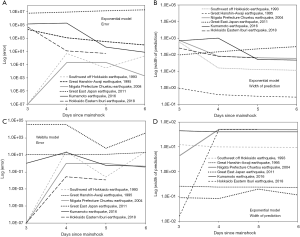
We also examined the percentile-based predictions, assuming that day 2 was the median number of days since the mainshock for all earthquakes. For the Southwest-off Hokkaido, Great Hanshin-Awaji, Niigata Prefecture Chuetsu, Great East Japan, Kumamoto, and Hokkaido Iburi Eastern earthquakes, with the observed death counts of 202, 5,502, 40, 15,897, 50, and 41, the median prediction yielded the forecasts (and errors) of 194 (–8), 5,886 (+384), 50 (+10), 1,376 (–14,521), 32 (–18), and 70 (+29) deaths, respectively. Figure 5A shows the error for different percentile points and earthquakes. Clearly, forecasts using the upper quartile yielded values that were closer to the observed number of deaths.
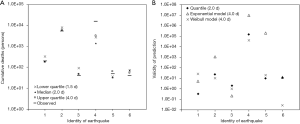
Figure 5B shows a comparison of the validity of the examined approaches using the exponential model, the Weibull model, and percentiles. The percentile method offered a median-based forecast on day 2, whereas the consistent convergence of the models was observed only on day 4 or later. Limited convergence is due to limited precision of the data and only six earthquakes that we were able to include. Although the percentile-based method was not always better, the extent of the error based on the median-based method was comparable with that based on the exponential and Weibull models. The percentile-based method yielded the best performance especially for the Southwest-off Hokkaido and Kumamoto earthquakes, even on day 2.
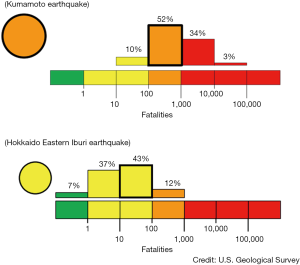
Figure 6 shows the PAGER results for the Kumamoto and Hokkaido Eastern Iburi earthquakes. The precision of forecasted fatalities was recorded by the power function of 10. According to PAGER, predicted deaths for the Kumamoto and Hokkaido Eastern Iburi earthquakes ranges from 100 to 1,000 persons and 10 to 100 persons, respectively, upon occurrence of earthquake. Because of the need for rapid response, precision is limited, and the distribution on a logarithmic scale was flat for both earthquakes. The actual fatalities of the Kumamoto earthquake corresponded to the third highest frequency, whereas the actual fatalities of the Hokkaido Eastern Iburi earthquake were well predicted as the highest frequency by PAGER.
Discussion
In the present study, we analyzed six earthquakes in Japan that involved at least 20 deaths occurring from 1990 to 2018. To analyze the statistical patterns in the cumulative number of deaths, we used three models (the exponential model, the Weibull model, and the percentile-based model) to predict the likely number of deaths during the early stage of earthquakes. For the evaluation, validity and reliability were assessed for the parametric models, whereas only validity was assessed for the percentile-based method. The parametric models started to converge from day 4; however, we found that all earthquakes except the Great East Japan earthquake reached the median number of deaths on day 2; that is, by multiplying the cumulative number of deaths as of day 2 by a factor of two, we could calculate the likely total number of deaths using the percentile-based method, and the validity of such a simple method was better than the results from day 4 using the parametric models. The Great East Japan earthquake was exceptionally large and involved a large number of fatalities caused by a tsunami; excluding this earthquake, the percentile-based method performed well, regardless of the year of the earthquake. Although our analysis of news media data involved reporting delays of up to 12 hours, the proposed method can be applied directly to police announcement data in the future.
As its most important contribution, the present study has empirically demonstrated that the likely size of a disaster can be assessed using data on direct deaths. In addition to direct deaths, fatalities during earthquakes also include indirect deaths, which are referred to as disaster-related deaths in Japan (21). Indirect deaths encompass the total number of deaths occurring because of environmental changes induced by the earthquake, which may lead to the exacerbation of chronic illnesses and diseases associated with mental distress. The present study focused on direct deaths, which reflect the immediate physical impact of the earthquake. We have shown that the immediate impact is partly measurable as of day 2 after the mainshock, and this could act as a benchmark for future evaluation. Moreover, our proposed simple method could help to quantify the required amount of medical resources, including the number of medical experts to be deployed (e.g., by determining the numbers of physicians and nurses to be deployed via J-DMAT). Considering that limited medical resources and delays in medical interventions during the early stage of earthquakes are known as triggers of indirect death (22), this quantitative method for helping people to make decisions regarding the required resources to dispatch may also have the potential to reduce disaster-related deaths.
The present study is not the first to propose a decision-making system that estimates potential losses caused by a natural disaster (23); Hazard United States (HAZUS), a useful visualization tool that uses a geographic information system, was developed by the Federal Emergency Management Agency and the National Institute of Building Sciences (24,25). Additionally, PAGER can produce estimates concerning the impact of significant earthquakes around the world (26). These systems can offer the forecasts in the first hour after the mainshock, which could be used to deploy rescue teams to mitigate the impact of the event. PAGER has shown that accounting for physical aspects of earthquakes (e.g., distance to the epicenter, rupture, propagation, population distribution, and building properties) as well as the timing of the earthquake (i.e., the hour of day when the earthquake occurs) greatly help in predicting the impact. When such data are lacking, our proposed method could be used for forecasting; this would require 2 days, but the forecasting could be achieved with minimal data requirements. Additional published methods include an integrated evaluation tool that uses engineering and epidemiological theories (27,28) and a system that predicts the number of deaths using a risk analysis method that measures social vulnerability (29-33). A system managed by the International Center for Earth Simulation called Quake Loss Assessment for Response and Mitigation (QLARM) (34) is also used for earthquake damage prediction (35-37). Of the existing methods, HAZUS has been routinely used in disaster medicine, and PAGER and QLARM offer estimates within 30 minutes of the mainshock, which is the expected timescale for prediction in physical science (38,39).
Notably, each of these existing methods requires multiple pieces of information as input variables for computation, whereas our proposed percentile method uses only the cumulative number of deaths. Thus, the practical contribution of our study to the field is that we have empirically shown the quickest method to analyze the observed number of deaths in Japan, where deaths are quickly identified after the mainshock and reported continuously.
Clearly, the prediction of the number of deaths during an earthquake would ideally include the underlying mechanisms of the particular earthquake. The essential pieces of information may be the geographic distribution of seismic intensity, landform type, seismic resistance and seismic isolated structure of buildings, social vulnerability, and healthcare infrastructure and access (26,29-37), which are inductively taken into account by PAGER and QLARM. The scientific analysis of such a rigorous series of data would ideally be performed; however, our analysis of the cumulative number of deaths omits these details in an attempt to capture general patterns of fatalities during large earthquakes. With the exception of extremely large earthquakes, such as the Great East Japan earthquake, we have shown that the cumulative number of deaths behaves similarly in the social setting of Japan (where different regions are characterized by a similar housing style, social vulnerability, and administrative mechanism to identify, report, and count the number of deaths). Exploiting these similarities, our proposed method could greatly help in determining the immediate number of medical experts and services to be deployed.
Several limitations of our study should be discussed. First, the prediction of the cumulative number of deaths using the proposed method is thus far restricted to Japan. If similar datasets are constructed in other countries, the prediction method could be considered for use in these additional contexts. Second, the proposed approach did not perform well for the Great East Japan earthquake. However, the validity of the percentile-based method for the 1995 Great Hanshin-Awaji earthquake, which was the second-largest earthquake examined in this study, did not deviate from that of the other earthquakes; thus, we believe that the size of the 2011 Great East Japan earthquake and the tsunami-induced deaths during this disaster were truly exceptional. Third, additional information, such as the age groups and geographic locations of the deceased individuals, could inform further methodological development in forecasting the cumulative number of deaths during earthquakes. Fourth, there was no uncertainty bound for the percentile-based method, and our reliability rests on six earthquakes and future updates would be indispensable.
Despite these limitations, we believe that the present study contributes greatly to forecasting the number of deaths during an earthquake. Even in settings with poor technical resources, the predicted number of deaths can be obtained by multiplying the reported cumulative number of deaths at noon on day 2 after the mainshock by a factor of two.
Conclusions
The present study analyzed six earthquakes in Japan that involved at least 20 deaths occurring from 1990 to 2018. By analyzing the statistical patterns in the cumulative number of deaths, we found that all the earthquakes except the Great East Japan earthquake reached the median number of deaths on day 2. By multiplying the cumulative number of deaths as of day 2 by a factor of two, it is possible to calculate the likely number of deaths using the percentile-based method. Although having physical and geographic datasets on the earthquake and the affected population would help us to measure the overall size of an earthquake event as quickly as within 1 hour, we believe that the present study greatly contributes to forecasting the number of deaths during an earthquake with minimal data requirements.
Acknowledgments
We thank Maxine Garcia, PhD, and Jennifer Barrett, PhD, from Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.
Funding: HN received funding from the Japan Agency for Medical Research and Development (AMED) (grant number: 19fk0108104 and JP20fk0108140), Environment Research and Technology Development Fund (JPMEERF20S11804), the Japan Society for the Promotion of Science (JSPS) KAKENHI (17H04701), Health and Labor Sciences Research Grants (19HA1003, 20CA2024, and 20HA2007), and the Japan Science and Technology Agency (JST) CREST program (grant number: JPMJCR1413).
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-5784
Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-5784). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. We analyzed publicly available data based on the headlines in newspapers; the analysis of publicly available data with no identifiable information did not require ethical approval.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Japan Institute of Country-ology and Engineering (JICE). Know the country. Unexpectedly unknown Japanese land. Available online: (Accessed 12 Dec 2019).http://www.jice.or.jp/knowledge/japan/commentary09
- Cabinet Office, Government of Japan. Disaster prevention information. Available online: (Accessed 12 Dec 2019).http://www.bousai.go.jp/kaigirep/hakusho/h31/honbun/3b_6s_08_00.html
- World Health Organization. Preparedness and public health response to disease outbreaks, natural disasters and other emergencies. Available online: (Accessed 12 Dec 2019).http://www.emro.who.int/about-who/public-health-functions/preparedness-and-public-health-response-to-disease-outbreaks-natural-disasters-and-other-emergencies.html
- Spiegel PB. Differences in world responses to natural disasters and complex emergencies. JAMA 2005;293:1915-8. [Crossref] [PubMed]
- Vasilescu L, Khan H, Khan A. Disaster management CYCLE – a theoretical approach. Manage Market J 2008;6:43-50.
- Thiel C, Schneider J, Hiatt D, et al. 9-1-1 EMS process in the Loma Prieta earthquake. Prehosp Disaster Med 1992;7:348-58. [Crossref]
- Brown DB, Smith MJ, Chibi MT, et al. Minimizing postdisaster fatalities. Fed Pract 2017;34:10-3. [PubMed]
- Arziman I. Field Organization and Disaster Medical Assistance Teams. Turk J Emerg Med 2016;15 Suppl 1:11-9. [PubMed]
- Fuse A, Yokota H. An analysis of Japan Disaster Medical Assistance Team (J-DMAT) deployments in comparison with those of J-DMAT's counterpart in the United States (US-DMAT). J Nippon Med Sch 2010;77:318-24. [Crossref] [PubMed]
- Parmar P, Arii M, Kayden S. Learning from Japan: strengthening US emergency care and disaster response. Health Aff (Millwood) 2013;32:2172-8. [Crossref] [PubMed]
- Simpson M, James R, Hall JW, et al. Decision analysis for management of natural hazards. Annual Rev Environ Res 2016;41:489-516. [Crossref]
- Song SY, Park JM. Development of damage prediction formula for natural disasters considering economic indicators. Sustainability 2019;11:868. [Crossref]
- Astoul A, Filliter C, Rau-Chaplin A, et al. Risk analytics for estimating and validating magnitude of earthquake losses. In: Los Alamitos: 24th International Workshop on Database and Expert Systems Applications, 2013.
- Guettiche A, Guéguen P, Mimoune M. Economic and human loss empirical models for earthquakes in the Mediterranean region, with particular focus on Algeria. Int J Disaster Risk Sci 2017;8:415-34. [Crossref]
- Oliver-Smith A, Alcántara-Ayala I, Burton I, et al. Forensic Investigations of Disasters (FORIN): a conceptual framework and guide to research. Beijing: Integrated Research on Disaster Risk, 2016.
- Kunz M, Zschau J, Wenzel F, et al. Forensic disaster analysis in near-real time. In: EGU General Assembly Conference Abstracts, 2014:16625.
- Miyake T. Magnitude, moment, and measurement: the seismic mechanism controversy and its resolution. Stud Hist Philos Sci 2017;65-66:112-20. [Crossref] [PubMed]
- Japan Meteorological Agency: Monitoring of earthquakes, tsunamis and volcanic activity. 2015. Available online: (Accessed 12 Dec 2019).https://www.jma.go.jp/jma/en/Activities/earthquake.html
- Japan Meteorological Agency: Tables explaining the JMA Seismic Intensity Scale. In: Monitoring of earthquakes, Tsunamis & Volcanic Activity, 2009. . Accessed 12 Dec 2019.https://www.jma.go.jp/jma/en/Activities/inttable.html
- Nikkei Telecom 21. Nikkei Inc. Tokyo. 1997. Available online: (Accessed 1 Oct 2019).https://t21.nikkei.co.jp/g3/CMN0F21.do
- Hayakawa M. Increase in disaster-related deaths: risks and social impacts of evacuation. Ann ICRP 2016;45:123-8. [Crossref] [PubMed]
- Yamanouchi S, Sasaki H, Tsuruwa M, et al. Survey of preventable disaster deaths at medical institutions in areas affected by the Great East Japan Earthquake: retrospective survey of medical institutions in Miyagi Prefecture. Prehosp Disaster Med 2017;32:515-22. [Crossref] [PubMed]
- Wyss M, Shroder JF. editors. Earthquake hazard, risk and disasters. New York: Academic Press, 2014:143-65.
- Federal Emergency Management Agency. HAZUS-MH MR4 technical manual: FEMA. 2003. Available online: (Accessed 12 Dec 2019).https://www.fema.gov/hazus
- Levi T, Bausch D, Katz O, et al. A. Insights from Hazus loss estimations in Israel for Dead Sea Transform earthquakes. Nat Hazards 2015;75:365-8. [Crossref]
- Porter K. Cracking an open safe: HAZUS vulnerability functions in terms of structure-independent spectral acceleration. Earthquake Spectra 2009;25:361-78. [Crossref]
- Jaiswal K, Eari M, Wald D. An empirical model for global earthquake fatality estimation. Earthquake Spectra 2010;26:1017-37. [Crossref]
- Shapira S, Aharonson-Daniel L, Shohet IM, et al. Integrating epidemiological and engineering approaches in the assessment of human casualties in earthquakes. Nat Hazards 2015;78:1447-62. [Crossref]
- Shapira S, Novack L, Bar-Dayan Y, et al. An integrated and interdisciplinary model for predicting the risk of injury and death in future earthquakes. PLoS One 2016;11:e0151111. [Crossref] [PubMed]
- Noriega GR, Ludwig LG. Social vulnerability assessment for mitigation of local earthquake risk in Los Angeles County. Nat Hazards 2012;64:1341-55. [Crossref]
- Peek-Asa C, Ramirez M, Seligson H, et al. Seismic, structural, and individual factors associated with earthquake related injury. Inj Prev 2003;9:62-6. [Crossref] [PubMed]
- Escaleras M, Anbarci N, Register CA. Public sector corruption and major earthquakes: a potentially deadly interaction. Public Choice 2007;132:209-30. [Crossref]
- Gutiérrez E, Taucer F, De Groeve T, et al. Analysis of worldwide earthquake mortality using multivariate demographic and seismic data. Am J Epidemiol 2005;161:1151-8. [Crossref] [PubMed]
- Rosset P, Bishop B, Tolis S, et al. QLARM: a Global Model for Earthquake Loss Estimatesin Real-Time and Scenario Modes. In: Geneva: UNISDR Science and Technology Conference on the implementation of the Sendai Framework for Disaster Risk Reduction 2015-2030, 2016.
- Trendafiloski G, Wyss M, Rosset P, et al. Constructing city models to estimate losses due to earthquakes worldwide: application to Bucharest, Romania. Earthquake Spectra 2009;25:665-85. [Crossref]
- Rosset P, Wyss M. Seismic loss assessment in Algeria using the tool QLARM. Civil Eng Res J 2017;2:555583. [Crossref]
- Fontiela J, Rosset P, Wyss M, et al. Human losses and damage expected in future earthquakes on Faial Island--Azores. Pure Appl Geophys 2020;177:1831-44. [Crossref]
- Satriano C, Elia L, Martino C, et al. PRESTo, the earthquake early warning system for Southern Italy: Concepts, capabilities and future perspectives. Soil Dynamics and Earthquake Engineering 2011;31:137-53. [Crossref]
- Caccavale M, Matano F, Sacchi M. An integrated approach to earthquake-induced landslide hazard zoning based on probabilistic seismic scenario for Phlegrean Islands (Ischia, Procida and Vivara), Italy. Geomorphology 2017;295:235-59. [Crossref]


