
Sources of bias for single-arm phase II cancer clinical trials
Introduction
Cancer clinical trials are to investigate the efficacy and toxicity of experimental cancer therapies. If an appropriate dose level of an experimental drug is determined from a phase I trial, the drug’s anticancer activity is assessed by phase II clinical trials. Through phase II clinical trials, inefficacious experimental therapies are screened out before proceeding to further investigation by large scale phase III trials.
In order to expedite this process, phase II trials popularly use a single-arm design to treat patients by experimental therapies only. By a single-arm trial, the efficacy of an experimental therapy is compared with that of a standard therapy with historical data. The most popular primary endpoint of phase II cancer clinical trials is tumor response which is measured by the change in tumor size before and during treatment. For a solid tumor, if the size, defined as sum of the largest diameter of the target tumor decreases by at least 30% compared to that at the baseline, we call it a partial response by RECIST 1.1 (1).
If the target tumor disappears during treatment, then we call it a complete response. Overall response is defined as partial or complete response.
The single-arm design is feasible only when reliable historical data are available for a selected control therapy. Historical data often come from a prior phase II trial that evaluated the efficacy of the current control therapy as an experimental therapy.
Phase II trials generally require shorter study periods than phase III trials. Consequently, phase II trials have small sample sizes, so that exact statistical methods are preferable to the asymptotic methods for their design and analysis. Various exact methods have been published for phase II trials with binary outcomes such as tumor response. For ethical reasons, two-stage designs with a futility stopping option are commonly used for phase II cancer clinical trials.
Let p0 denote the response rate of a historical control, and p1 denote a response rate of interest for an experimental therapy. A single-arm two-stage trial, that is specified by sample sizes n1 and n2 for stages 1 and 2, respectively, futility stopping value a1, and stage 2 critical value a, is conducted as follows.
- Stage 1: Treat n1 patients and count the number of responders X1.
- If X1 ≤ a1, then reject the experimental therapy and stop the trial.
- Otherwise, proceed to the second stage.
- Stage 2: Treat an additional n2 patients and count the number of responders X2.
- If X1 + X2 ≤ a, then reject the experimental therapy.
- Otherwise, accept the experimental therapy for further investigation.
We usually do not stop the trial early for superiority since there is no ethical issue to continue treating patients with an efficacious therapy and we want to collect as much data as possible to use when designing a subsequent phase III trial.
For the true response rate p, X1 and X2 are independent binary random variables with a common success probability p and number of trials n1 and n2, respectively. Using this fact, we can calculate the type I error rate (or false positivity) and the power (or true positivity) for a given two stage design, (n1, n2, a1, a). Given (α, 1− β), any two-stage design with a type I error rate smaller than or equal to α and a power larger than or equal to 1− β is called a candidate design. Among the candidate designs, the one with the smallest maximal sample size n = n1 + n2 is called the minimax design and the smallest expected sample size when p = p0 is called the optimal design by Simon (2). When the minimax and optimality criteria result in very different two-stage designs, Jung et al. (3,4) propose admissible designs minimizing linear combinations of maximal sample size and expected sample size for p = p0.
When a two-stage phase II trial is completed, the sample proportion calculated using the cumulative data up to the stopping stage is usually reported as an estimate of the true response rate of the experimental therapy. For a two-stage design with a futility stopping only, this estimator is negatively biased because the numbers of responders larger than the futility limit are not observed if the stopping stage is 1. This is the first issue we want to discuss in this article.
Oftentimes, the patient population of a single-arm phase II trial consists of multiple subpopulations with different level of expected response rates. In this case, the standard design and analysis method based on an unstratified testing can seriously amplitude the type I error rate or deplete the statistical power depending on the number of patients accrued from different subpopulations. This is the second issue to be discussed in this review paper. We discuss alternative design and analysis methods that are proposed to overcome these bias issues.
Biased estimation of response rate
In a single-stage phase II trial, the sample proportion of response rate is an unbiased estimator. However, in a multi-stage phase II trial, this is not the case.
In this section, we focus on the popular two-stage designs with a futility interim test. For a two-stage design, the values of (a1/n1, a/n) are determined based on some prespecified design parameters as described below. Let p0 denote the maximum unacceptable probability of response which is usually chosen by the RR of a historical control, and p1 the minimum acceptable probability of response with p0 < p1. For the true RR p of the experimental therapy, we want to test H0: p ≤ p0 against H1: p > p0. In this statistical testing, rejecting H0 means accepting the experimental therapy. Given (p0, p1), we can calculate the type I error rate α and power 1− β of a two-stage design (a1/n1, a/n) based on the fact that the number of responders from the two stages, X1 and X2, are independent binomial random variables.
Let M denote the stopping stage, and S = SM denote the total number of responders accumulated up to the stopping stage, so that we have S = X1 if M = 1 and S = X1 + X2 if M = 2. For (M, S) = (m, s), most publications of two-stage phase II trials report the sample proportion
as an estimator of the true response rate p of the study therapy. The sample proportion is the maximum likelihood estimator (MLE) of p. Jung and Kim (5) show that, for two-stage phase II trials, the MLE has bias
From Eq. [2], the bias depends on (n1, n, a1), but not on a. From Simon (2) and Jung et al. (4), a1 is usually close to n1p0, so that x1 − n1p will be negative for 0 ≤ x1 ≤ a1 and p > p0. Hence, for a two-stage phase II trial with a futility stopping only, the bias of MLE is negative.
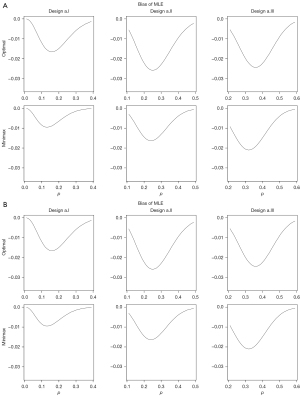
We investigate two sets of numerical studies to evaluate the bias of MLE. In the first set of numerical studies (a), we consider Simon’s optimal and minimax designs [a1/n1, a2/(n1 + n2)] with (α, β) = (0.05, 0.1) for the following binomial probabilities.
- p0 =0.1 and p1 =0.3: optimal = (2/18, 6/35), minimax = (2/22, 6/33);
- p0 =0.2 and p1 =0.4: optimal = (4/19, 15/54), minimax = (5/24, 13/45);
- p0 =0.3 and p1 =0.5: optimal = (8/24, 24/63), minimax = (7/24, 21/53).
These numerical studies were conducted to evaluate the bias of the MLE for different values of the true binomial probability.
In the second set of numerical studies (b), we considered Simon’s optimal and minimax designs to test p0 =0.2 vs. p1 =0.4 with the following type I and II error probabilities.
- α =0.1 and β =0.1: optimal = (3/17, 10/37), minimax = (3/19, 10/36);
- α =0.05 and β =0.2: optimal = (3/13, 12/43), minimax = (4/18, 10/33);
- α =0.05 and β =0.1: optimal = (4/19, 15/54), minimax = (5/24, 13/45).
These numerical studies were to evaluate the bias of the MLE for different values of the type I and II error probabilities.
Figure 1A,1B displays bias of the MLE for designs a.I, a.II and a.III and for designs b.I, b.II and b.III, respectively, for a range of true p values including p0 and p1. Note that the maximum bias occurs for p between p0 and p1, but closer to p0. Compared to minimax designs, optimal designs tend to conduct the interim analysis earlier to minimize the expected sample size, so that n2/n1(n1 + n2) in Eq. [2], and hence the absolute value of bias, is larger for optimal designs. The bias seems to increase as p0 and p1 get close to 0.5.
Oftentimes, the MLE from a former two-stage phase II trial is used as p0 value for a new phase II trial on an experimental therapy. In this case, if p0 is underestimated by using the MLE from a former phase II trial, the new trial will have an increased false positivity.
If one wants to avoid a bias one may use the uniformly minimum-variance unbiased estimator (UMVUE) that is given as
where a ∧ b = min(a, b) and a ∨ b = max(a, b). Note that the UMVUE is identical to the MLE if M = 1. While UMVUE is unbiased estimator of p, its efficiency is comparable to that of MLE (5).
By Jung and Kim (5), the probability mass function of the random vector (M, S) for a two-stage design with (a1/n1, a/n) is given by
Example 1: suppose that a standard therapy has a response rate of p0 =20% and an experimental therapy will be of interest if its response rate is p1 =40% or higher. In this setting, we consider a two-stage design with (a1/n1, a/n) = (3/13, 12/43). This design is optimal according to Simon (2) for p0 =20% and p1 =40% with α=0.05 and power 1− β =0.8. Table 1 lists the UMVUE and the MLE for observations from this two-stage design. When m =1, two estimates are exactly the same as noted earlier. When m =2, the MLE is much smaller than UMVUE for small s values. We also calculated the probability mass function f (m, s|p) of (M, S) for the true response rates p =0.1:0.5:0.1. For the outcomes of (M, S) for which the MLE is very different from UMVUE, the probability mass functions are not very large for any true response rates considered here, so that the bias of MLE cannot be very big. In this example, the bias of MLE is −0.0054, −0.0264, −0.0351, −0.0238, and −0.0094 when the true response rate is p=0.1, 0.2, 0.3, 0.4, and 0.5, respectively.
Table 1
| m | s | UMVUE | MLE | f(m, s|p) for p | ||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||||
| 1 | 0 | 0.000 | 0.000 | 0.254 | 0.055 | 0.010 | 0.001 | 0.000 |
| 1 | 1 | 0.077 | 0.077 | 0.367 | 0.179 | 0.054 | 0.011 | 0.002 |
| 1 | 2 | 0.154 | 0.154 | 0.245 | 0.268 | 0.139 | 0.045 | 0.010 |
| 1 | 3 | 0.231 | 0.231 | 0.100 | 0.246 | 0.218 | 0.111 | 0.035 |
| 2 | 4 | 0.308 | 0.093 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 5 | 0.312 | 0.116 | 0.004 | 0.002 | 0.000 | 0.000 | 0.000 |
| 2 | 6 | 0.317 | 0.140 | 0.007 | 0.006 | 0.001 | 0.000 | 0.000 |
| 7 | 0.322 | 0.163 | 0.008 | 0.015 | 0.002 | 0.000 | 0.000 | |
| 2 | 8 | 0.328 | 0.186 | 0.006 | 0.027 | 0.006 | 0.000 | 0.000 |
| 2 | 9 | 0.335 | 0.209 | 0.004 | 0.038 | 0.015 | 0.001 | 0.000 |
| 2 | 10 | 0.343 | 0.233 | 0.002 | 0.043 | 0.030 | 0.003 | 0.000 |
| 2 | 11 | 0.351 | 0.256 | 0.001 | 0.041 | 0.049 | 0.008 | 0.000 |
| 2 | 12 | 0.360 | 0.279 | 0.000 | 0.033 | 0.068 | 0.018 | 0.001 |
| 2 | 13 | 0.371 | 0.302 | 0.000 | 0.023 | 0.081 | 0.033 | 0.003 |
| 2 | 14 | 0.382 | 0.326 | 0.000 | 0.014 | 0.084 | 0.054 | 0.006 |
| 2 | 15 | 0.395 | 0.349 | 0.000 | 0.007 | 0.076 | 0.076 | 0.013 |
| 2 | 16 | 0.409 | 0.372 | 0.000 | 0.003 | 0.062 | 0.096 | 0.025 |
| 2 | 17 | 0.424 | 0.395 | 0.000 | 0.001 | 0.044 | 0.107 | 0.042 |
| 2 | 18 | 0.440 | 0.419 | 0.000 | 0.001 | 0.029 | 0.108 | 0.063 |
| 2 | 19 | 0.458 | 0.442 | 0.000 | 0.000 | 0.017 | 0.098 | 0.085 |
| 2 | 20 | 0.477 | 0.465 | 0.000 | 0.000 | 0.009 | 0.080 | 0.105 |
| 2 | 21 | 0.496 | 0.488 | 0.000 | 0.000 | 0.004 | 0.059 | 0.116 |
| 2 | 22 | 0.517 | 0.512 | 0.000 | 0.000 | 0.002 | 0.040 | 0.118 |
| 2 | 23 | 0.538 | 0.535 | 0.000 | 0.000 | 0.001 | 0.025 | 0.108 |
| 2 | 24 | 0.560 | 0.558 | 0.000 | 0.000 | 0.000 | 0.014 | 0.091 |
| 2 | 25 | 0.582 | 0.581 | 0.000 | 0.000 | 0.000 | 0.007 | 0.069 |
| 2 | 26 | 0.605 | 0.605 | 0.000 | 0.000 | 0.000 | 0.003 | 0.048 |
| 2 | 27 | 0.628 | 0.628 | 0.000 | 0.000 | 0.000 | 0.001 | 0.030 |
| 2 | 28 | 0.651 | 0.651 | 0.000 | 0.000 | 0.000 | 0.001 | 0.017 |
| 2 | 29 | 0.674 | 0.674 | 0.000 | 0.000 | 0.000 | 0.000 | 0.009 |
| 2 | 30 | 0.698 | 0.698 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 |
| 2 | 31 | 0.721 | 0.721 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 |
| 2 | 32 | 0.744 | 0.744 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 2 | 33 | 0.767 | 0.767 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 34 | 0.791 | 0.791 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 35 | 0.814 | 0.814 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 36 | 0.837 | 0.837 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 37 | 0.861 | 0.861 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 38 | 0.884 | 0.884 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 39 | 0.907 | 0.907 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 40 | 0.930 | 0.930 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 41 | 0.954 | 0.954 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 42 | 0.977 | 0.977 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 43 | 1.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
UMVUE, uniformly minimum-variance unbiased estimator; MLE, maximum likelihood estimator.
Single-arm trials for heterogeneous patient population
Usually, phase II clinical trials are designed assuming that the patient population is homogeneous so that all patients have an equal response rate p as in the previous section. More often than not, however, a study population has multiple subpopulations in terms of the level of prognosis, so that the expected response rate is different among the subpopulations.
Example 2: in a phase II trial to evaluate the tumor response of CD30 antibody, SGN-30, combined with GVD (Gemcitabine, Vinorelbine, Pegylated Liposomal Doxorubicin) chemotherapy in patients with relapsed or refractory classical Hodgkin lymphoma (HL), the study population includes both patients who never had a bone marrow transplant and those who had one. In a previous study, GVD only led to responses in 65% among those who never had a transplant and 75% in the transplant group. About γ1 =50% of patients in the previous study never had a transplant. Combining the data from the two subpopulations, the response rate for the whole patient population is estimated as 70% (=0.5×0.65+0.5×0.75).
Using this outcome as historical control data, the new study is designed as a single-arm trial for testing
where p denotes the true RR of the combination therapy in the patient population combining the two subpopulations, one for those with prior transplants and the other for those without one.
A standard design to account for the heterogeneity of the patient population is a single-arm trial based on a specified prevalence for each subpopulation for testing hypotheses Eq. [5]. For the example study, we consider an increase in response rate by 15% or larger clinically significant for each subpopulation. So, we will not be interested in the combination therapy if the true response rate, p, is lower than p0 =70% and will be strongly interested if the true response rate is higher than pa =85%. Then, the Simon’s (2) two-stage optimal design for testing
with type I error rate no larger than α∗ =0.1 and power no smaller than 1− β∗ =0.9 is = (14/20, 45/59), where and denote the fixed (unstratified) rejection values for stages 1 and 2, respectively.
Let Xkj denote the number of responders among mkj patients who were recruited from subpopulation j (= 1, 2) during stage k (= 1, 2). Note that mk1 + mk2 = nk. For the true response rate pj for subpopulation j, (Xkj, k =1, 2, j =1, 2) are independent binomial random variables with B(mkj, pj). Based on this, we can calculate the type I error rate and the statistical power conditioning on the observed frequency mkj. Figure 2A displays type I error rate and power (thin lines) with respect to the number of patients mk1 without a prior transplant recruited during stage k (= 1, 2). The x-axis is marked for m11 values in [0, 20], but m21 (∈ [0, 39]) values run between two consecutive m11 values. The power curve of the stratified test has waves with a length of one unit of m11, and each wave consists of saw teeth with a length of one unit of m21. The waves have a bigger cycle that changes when the futility stopping value is changed depending on m11 values. We observe that the true type error rate fluctuates between 0.018 (when all patients had no prior transplant, i.e., m11 =20 and m21 =39) and 0.311 (when all patients had prior transplant, i.e., m11 = m21 =0). Similarly, the power changes between 0.645 and 0.988. If the observed frequency is close to the specified γ1 =50% (i.e., m11 ≈ n1γ1 =10 and m21 ≈ n2γ1 =19.5), then the type I error rate and power are close to the specified 0.05 and 0.9, respectively.
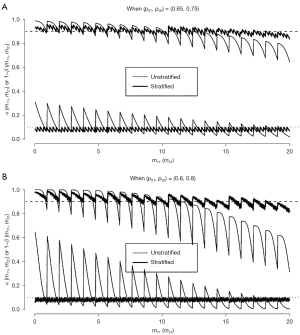
Note that the rejection values and are fixed regardless of observed values of mk1 for k=1, 2. In order to account for the observed prevalence for each subpopulation, London and Chang (6) and Jung et al. (7) propose stratified analysis methods. Especially, Jung et al. (7) propose to change the rejection values a1 and a depending on the observed values of m11 and m21 as follows.
- Step 1: specify (p01, p02, pa1, pa2), γ1, and (α∗, 1− β∗).
- Step 2: for p0 = γ1p01 + γ2p02 and pa = γ1pa1 + γ2pa2, choose a standard (unstratified) two-stage design for testing
- that satisfies the (α∗, 1− β∗)-condition. We use (n1, n2) for the chosen standard design as the stage 1 and 2 sample sizes of the stratified design.
- Step 3: after stage 1, calculate a1 = a1(m11) = [m11p01 + m12p02] based on the observed m11, where [x] denotes the rounddown of x. We reject the therapy if x1 = x11 + x12 is smaller than or equal to a1(m11). Otherwise, we proceed to stage 2.
- Step 4: after stage 2, choose the maximum a = a(m11, m21) satisfying α(m11, m21) ≤ α∗ based on (m11, m21). Accept the therapy if x = x11 +x12 +x21 +x22 is larger than a(m11, m21).
- Step 5: calculate the conditional power 1− β(m11, m21) for a two-stage design (n1, m11, n2, m21, a1, a).
Before closing patient accrual, we may check the power of the selected two-stage design based on the observed (m11, m21) and consider recalculating the stage 2 sample size n2 based on the observed prevalence for an appropriate power.
Figure 2A also displays the type I error rate and power (thick lines) of the stratified two-stage design with (n1, n) = (20, 59) for (p01, p02, pa1, pa2) = (0.65, 0.75, 0.8, 0.9). We observe that, regardless of observed (m11, m21) values, the stratified two-stage design controls the type I error rate and power very closely to the specified α =0.1 and 1− β =0.9, respectively.
In this example, the difference between two subpopulations is only 10%(= p02 − p01 = pa2 − pa1). If this difference is bigger, the impact of stratified analysis becomes more noticeable. For example, suppose that the historical control, GVD alone, has a response rate of p01 =60% for patients with no prior transplant and p02 =80% for patients with a prior transplant, and the experimental combination therapy will be of interest if its response rate is at least pa1 =75% and pa2 =95% for the two subpopulations. Note that the difference in response rate is 20% between the two subpopulations in this case, while the amount of increase in response rate by the experimental therapy is 15% (= paj− p0j) for each subpopulation as in Example 2. Assuming the same prevalence γ1 =50%, the standard (unstratified) two-stage design will be identical with (a1/n1, a/n) = (14/20, 45/59) for (p0, pa, α, 1− β) = (0.7, 0.85, 0.1, 0.9) as in Example 2.
Figure 2B reports the type I error rate and power for both unstratified (thin lines) and stratified (thick lines) two-stage tests. Note that, while the stratified test controls type I error rate and power closely to the specified levels (α, 1− β) = (0.1, 0.9), those of unstratified test fluctuate more widely between 0.002 and 0.645 for the type I error rate and between 0.311 and 1.000 for power depending on (m11, m21) values. Regarding the shape of these curves, a tiny sawtooth occurs when a1 value changes and a big sawtooth occurs when a value changes. While a1 changes between 13 and 15 and a change between 43 and 48 in Figure 2A, a1 changes between 12 and 16 and a change between 40 and 51 in Figure 2B.
Discussion
For phase II cancer clinical trials, most popular is single-arm two-stage design with a futility early stopping. In this paper, we have investigated two sources of bias for standard design and analysis methods of such trials.
At first, we have shown that the MLE, the sample proportion, to estimate the true response rate is negatively biased for two-stage designs with a futility stopping only. When a new single-arm phase II trial is designed for a new experimental therapy in the future, the underestimated response rate from the current trial will be used as a historical control, p0, so that the future trial will have a higher chance to accept the new experimental therapy and will lead to a large randomized trial that has a higher chance of failure even when the improvement in response rate is clinically negligible. In this paper, we focused on the point estimation of the true response rate for two-stage single-arm phase II trials. Porcher and Desseaux (8), Jung (9), and Grayling and Mander (10) discuss more inferential problems, such as P value and confidence interval, that can be subject to bias when the analysis of a single-arm phase II trial does not appropriately account for the two-stage design.
As a reviewer claims, the MLE, the sample proportion ignoring the multi-stage design, is intuitive and its bias is not be very large for the discussed example designs. Because of the bias, however, MLE has some undesirable properties. For example, the statistical testing results from confidence interval and P value calculated based on MLE-ordering may not match with that based on the critical values of a two-stage design. This mismatch comes from the fact that MLE does not account for the multi-stage design. On the other hand, the testing results from confidence interval and P value based on UMVUE-ordering always match with that based on the two-stage design (9). Jung et al. (11) show that the bias-corrected MLE (12) has the same ordering as UMVUE, so that they will give us identical testing results. Nevertheless, the bias-corrected MLE is still a biased estimator.
We have not considered two-stage designs with a superiority stopping, but the MLE from these trials will be positively biased. Also, the MLE will be more biased in studies with one-sided stopping boundaries than in those with lower and upper boundaries. Chang et al. (13) provides an excellent study of bias of the MLE in studies with lower and upper boundaries proposed by Chang et al. (14). To avoid the bias, we had better use the UMVUE that was proposed by Jung and Kim (4).
We also have investigated design of single-arm phase II trials for patient populations consisting of multiple subpopulations with different expected response rates. In this case, the standard (unstratified) single-arm design based on the weighted average of response rates for the whole population can result in severely biased type I error rate or statistical power unless the distribution of patient characteristics is similar between the new phase II trial and a selected historical control, which is hard to guarantee. We can always avoid this type of bias by using a stratified testing procedure. Although we have considered the cases with two subpopulations only, extension to cases with more than two subpopulations is straightforward. We have focused on two-stage designs, but the standard unstratified analysis method is biased in designs with any number of stages, including single-stage designs. A user-friendly graphical program to discover optimal two-stage designs for stratified testing is available to readers upon request.
Another robust solution to this kind of biases is to use a randomized phase II trial. Definitely, a randomized trial resolves most of the issues including these. It is very costly, however. Table 2 lists the maximal sample size n = n1 + n2 of single-arm two-stage phase II trials, taken from Table 1 of Simon (2), and randomized trials by Jung (15) for (α, 1− β, p1 − p0) = (0.1, 0.9, 0.2). We find that a two-arm randomized trial with a prospective control requires about 4 times, but not just twice, larger sample size than a single-arm trial. This relationship holds for any input parameter values of (p0, p1, α, 1− β). If there are no reliable historical control data, however, randomized phase II trial may be the only option. Grayling et al. (16) and the references therein extensively discuss favorable designs between sing-arm and randomized phase II trials under various scenarios.
Table 2
| p0 | p1 | Minimax | Optimal | |||
|---|---|---|---|---|---|---|
| 1-arm | 2-arm | 1-arm | 2-arm | |||
| 0.05 | 0.25 | 20 | 55 | 24 | 55 | |
| 0.10 | 0.30 | 25 | 55 | 35 | 55 | |
| 0.20 | 0.40 | 36 | 61 | 37 | 73 | |
| 0.30 | 0.50 | 39 | 76 | 46 | 85 | |
| 0.40 | 0.60 | 41 | 82 | 46 | 95 | |
| 0.50 | 0.70 | 39 | 81 | 45 | 95 | |
| 0.60 | 0.80 | 45 | 74 | 53 | 81 | |
Total sample size for a 2-arm trial is 2×n.
Acknowledgments
Funding: None.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors [Yanhong Deng, Qian Shi and Jun (Vivien) Yin] for the series “Challenges in Clinical Trials” published in Annals of Translational Medicine. The article has undergone external peer review.
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at https://atm.amegroups.com/article/view/10.21037/atm-21-6808/coif). The series “Challenges in Clinical Trials” was commissioned by the editorial office without any funding or sponsorship. The author has no other conflicts of interest to declare.
Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur J Cancer 2009;45:228-47. [Crossref] [PubMed]
- Simon R. Optimal two-stage designs for phase II clinical trials. Control Clin Trials 1989;10:1-10. [Crossref] [PubMed]
- Jung SH, Carey M, Kim KM. Graphical search for two-stage designs for phase II clinical trials. Control Clin Trials 2001;22:367-72. [Crossref] [PubMed]
- Jung SH, Lee T, Kim K, et al. Admissible two-stage designs for phase II cancer clinical trials. Stat Med 2004;23:561-9. [Crossref] [PubMed]
- Jung SH, Kim KM. On the estimation of the binomial probability in multistage clinical trials. Stat Med 2004;23:881-96. [Crossref] [PubMed]
- London WB, Chang MN. One- and two-stage designs for stratified phase II clinical trials. Stat Med 2005;24:2597-611. [Crossref] [PubMed]
- Jung SH, Chang MN, Kang SJ. Phase II cancer clinical trials with heterogeneous patient populations. J Biopharm Stat 2012;22:312-28. [Crossref] [PubMed]
- Porcher R, Desseaux K. What inference for two-stage phase II trials? BMC Med Res Methodol 2012;12:117. [Crossref] [PubMed]
- Jung SH. Statistical issues for design and analysis of single-arm multi-stage phase II cancer clinical trials. Contemp Clin Trials 2015;42:9-17. [Crossref] [PubMed]
- Grayling MJ, Mander AP. Two-Stage Single-Arm Trials Are Rarely Analyzed Effectively or Reported Adequately. JCO Precis Oncol 2021;5:PO.21.00276.
- Jung SH, Owzar K, George SL, et al. P-value calculation for multistage phase II cancer clinical trials. J Biopharm Stat 2006;16:765-75; discussion 777-83. [Crossref] [PubMed]
- Whitehead J. On the bias of maximum likelihood estimation following a sequential test. Biometrika 1986;73:573-81. [Crossref]
- Chang MN, Wieand HS, Chang VT. The bias of the sample proportion following a group sequential phase II clinical trial. Stat Med 1989;8:563-70. [Crossref] [PubMed]
- Chang MN, Therneau TM, Wieand HS, et al. Designs for group sequential phase II clinical trials. Biometrics 1987;43:865-74. [Crossref] [PubMed]
- Jung SH. Randomized phase II trials with a prospective control. Stat Med 2008;27:568-83. [Crossref] [PubMed]
- Grayling MJ, Dimairo M, Mander AP, et al. A Review of Perspectives on the Use of Randomization in Phase II Oncology Trials. J Natl Cancer Inst 2019;111:1255-62. [Crossref] [PubMed]


