
This article has an erratum available at: http://dx.doi.org/10.21037/atm-2022-10 the article has been update on 2022-04-25 at here.
Computational numerical analysis of different cannulation methods during cardiopulmonary bypass of type A aortic dissection model based on computational fluid dynamics
Introduction
Type A aortic dissection (TAAD) is a critical illness that requires emergency surgery and cardiopulmonary bypass (CPB) to reduce mortality related to various complications, such as the rupture of aortic dissection, acute myocardial ischemia, shock, and the insufficient perfusion of vital organs (1). Timely CPB surgery can result in good prognoses, even among elderly and/or pregnant TAAD patients (2,3). The use of CPB with hypothermic and/or moderate hypothermic circulatory arrest is still the gold standard in clinical practice (4). In CPB surgery, the femoral artery is undoubtedly the easiest artery on which to operate; however, this can also result in many postoperative complications, including stroke, thrombosis, and insufficient multiorgan perfusion due to plaque shedding, false lumen blood supply during retrograde perfusion (5). Axillary artery cannulation (AAC) is preferred to femoral artery cannulation (FAC) for antegrade perfusion to prevent visceral malperfusion (6). However, AAC also has a number of disadvantages; for example, it requires a more precise surgical technique, it is more time consuming, and it carries risks, such as upper extremity ischemia, local nerve injury, seroma, and restricted perfusion flow (7). For these reasons, some aortic surgeons are inclined to use innominate artery cannulation (IAC) in aortic arch repair. Further, IAC also allows the entire aortic arch repair surgery to be carried out after median sternotomy without any extra incisions. This type of centralized arterial cannulation strategy could streamline the surgical process, is easy to perform, and minimizes complications in TAAD (8,9). Although a meta-analysis showed that a similar neuroprotective outcome between IAC and AAC (10), some scholars still believed that IAC could lead to the potential risk of cerebral embolism due to higher antegrade flow or a new dissection and/or stenosis after the closure of the arteriotomy following decannulation (11). In addition, IAC is not recommended for patients with a second surgery, innominate artery dissection, and/or calcification (12).
There does not appear to have a better way of comparing the differences between different cannulations than summarizing the clinical data. That is, we do not know the specific state of blood flow under different cannulation modes. TAAD is a complex entity, for example, the entry and re-entry tear, extension of dissection, and the involvement of visceral vessels (13). Therefore, it is difficult to understand the complexities of flow dynamic perfusion. However, computational fluid dynamics (CFD) may provide insight (14).
Blood flow analysis by CFD is an advanced computing simulation tool that can be used to evaluate wall shear stress, stress, flow velocity, flow streamline, helicity index, and other fluid dynamic parameters (15). CFD has developed rapidly in recent years, and has been applied to the fields of medical bioengineering and cardiovascular disease (16). Although there were some studies on the CFD of aortic dissection, most of them focus on the CFD characteristics of the disease model and/or the CFD difference between preoperative and postoperative in type B, and there were few reports on the difference of CFD between different cannulation during CPB (17,18). In view of the correlation between cannulation and intraoperative perfusion and postoperative prognosis (19), therefore, in order to better understand this, we used CFD based on fluid-solid coupling models to analyze the hemodynamic characteristics of 3 different cannulation methods to facilitate clinical decision-making.
We present the following article in accordance with the MDAR reporting checklist (available at http://dx.doi.org/10.21037/atm-21-605).
Methods
Reconstruction of the TAAD model
A 46-year-old man (80 kg) was diagnosed with TAAD in cardiovascular surgery department which belongs to the people’s hospital of Gaozhou. Because this is a representative case of TAAD, the CFD model was reconstructed based on his CT data. The ultrasound results showed that the inner diameter of the ascending aorta had widened, the intimal line echo could be seen in the lumen, and the inner diameter of the pulmonary artery was normal. There was a small amount of regurgitation of the aortic valve (flow rate was 1 m/s and the pressure difference was 4 mmHg). Computed tomography angiography (CTA) results showed that the dissection (entry tear) was located on the ascending aorta, extending the aortic arch, descending aorta to the left common iliac artery (exit tear). The right renal artery, the celiac trunk, and superior mesenteric artery originate from the true lumen, and the left renal artery originate from the false lumen. The right renal artery perfusion was normal, but the left renal artery perfusion was reduced due to renal artery dissection.
Based on the patient’s CTA data, Mimics software (version 17.0; Materialise, Belgium) was used to perform a 3D reconstruction of the aorta. The model comprised the root of the aorta to the femoral artery, including the coronary artery, brachiocephalic artery, left common carotid artery, left subclavian artery, left and right renal arteries, and left and right femoral arteries. The blood vessel wall was divided into 3 layers, and the aortic fluid and solid models were imported into Hypermesh (version 2019) software to generate hexahedral and tetrahedral structures and fluid meshes. The meshing file was then transferred to ADINA software (version 9.6, USA) for the fluid-structure coupling calculation. The insertion of an 8-mm cannula into each of the different models was simulated. This model involving 2 tears. The entry tear was located on the ascending aorta, and the exit tear was located on the left iliac artery. Other multiple communicating tears and/or secondary tears were not involved in this model (Figure 1).
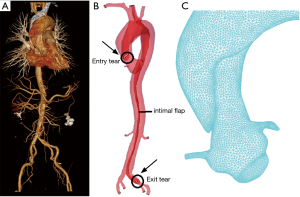
All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by ethics board of Gaozhou Hospital (No. GYLLYJ-2020014) and informed consent was taken from the patient.
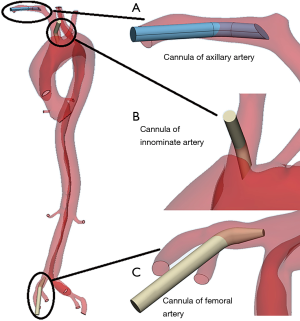
Arterial cannulation strategy
To obtain more realistic cannulation blood flow data during CPB, we simulated 3 types of cannulations (AAC, IAC, and FAC) in 2 CPB phases (Figure 2). In the early stage of the CPB, the heart and the cannula provide blood at the same time [cardiac output (CO) 2.5 L/min and CPB 2.5 L/min, defined as condition A]. System blood is only provided by the cannula (CO 0 L/min and CPB 5 L/min, defined as condition B). A comparison was made to determine the hemodynamic differences between these 2 conditions in which different cannulation methods were used.
Numerical scheme of fluid-structure interaction (FSI)
The FSI model was adopted to solve the interplay between the solid and fluid domains. We adopted the FSI simulation form in our study to obtain more realistic simulation data. The FSI was determined as follows:
where df is blood displacement, ds ds is left ventricular wall displacement, Tf is pressure on the blood, Ts is pressure on the wall of the left ventricle, and n indicates the normal direction of the corresponding interface.
The constitutive model of the blood vessel wall is defined as an anisotropic Mooney–Rivlin model. The strain energy density function is determined as follows:
where I1 is the first invariant, I2 is the second invariant, I4 is the circumferential unit vector, and c1 c2 D1 D2 K1 K2 are the parameters of the constitutive model.
Boundary conditions
In the present study, the patient’s aortic valve blood flow rate was used as the inlet boundary condition, and the CPB was set to a constant speed (as shown by the solid and dashed lines, respectively, in Figure 3). Given the average pressure at each outlet of the aortic model, a 70-mmHg pressure boundary condition was applied. The blood was set as an incompressible viscous Newtonian fluid. Blood density was 1,050 kg/m3, and viscosity was 0.0035 Pa·s (20).
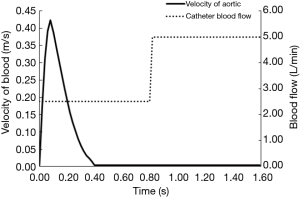
The cycle-independent results showed that the 3 cardiac cycles reached stability. Therefore, the 2 situations in the present study were examined in relation to the 3 cycles, and the hemodynamic results of the 3rd cardiac cycle were extracted for the hemodynamic analysis. The cardiac cycle time was set at 0.8 s, and the calculation time step was set at 8 ms.
Hemodynamic parameter collection and analysis
To clarify the changes in the hemodynamic status caused by different cannulation methods, we analyzed the blood flow of the main organ blood supply arteries under different conditions, the blood flow velocity at the breach (entry tear, exit tear), the change and distribution of shear stress, and the stress distribution (see Figures 4-8).
Statistical analysis
Data are expressed as the mean ± standard deviation for continuous data with a normal distribution, as the median for continuous data with a non-normal distribution. These analyses were performed using IBM SPSS software version 23.0.
Results
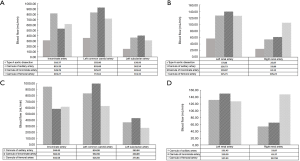
The result of the changes in blood flow volume under different conditions in the 3 cannulation methods
Figure 4 showed that in condition A, where blood flow had a CO of 2.5 L/min and a CPB of 2.5 L/min, blood flow was highest in AAC. The total flow for the branches of the aortic arch was 2,009.5 mL/min, 1,855.47 mL/min, and 1,648.03 mL/min for ACC, IAC, and FAC, respectively. All of the cannulation methods improved left renal blood perfusion; however, in relation to blood flow in the right renal artery, FAC had the highest blood flow (105 mL/min). In condition B, where the blood flow had a CO of 0 L/min and a CPB of 5 L/min, the results were similar to those of condition A. In addition, these 2 conditions before and after cardiac arrest had no significant effect on the blood flow of the 3 different cannulation methods.
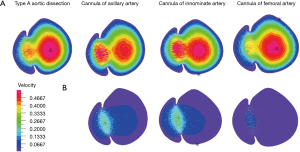
The result of the changes in blood flow velocity at the ascending aorta breach (entry tear)
Figure 5 showed that AAC had the highest blood velocity at the ascending aorta breach in conditions A and B. In condition A, the maximum flow velocity of breach in TAAD was 0.5588 m/s, the maximum blood flow velocity of AAC and IAC appeared in the false lumen (0.6256 and 0.6294 m/s, respectively), and the maximum blood flow velocity of FAC appeared in the true cavity (0.5343 m/s). In condition B, the maximum blood flow velocity of AAC and IAC occurred in the false cavity (0.2044 and 0.2363 m/s, respectively), while the maximum blood flow velocity of FAC occurred in the true lumen (0.0489 m/s). Compared with condition A, the velocity of AAC and IAC was lower in condition B.
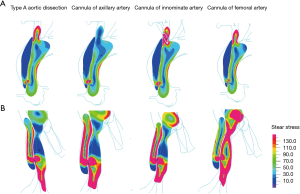
The result of the changes in wall shear stress distribution at the ascending aorta breach in condition A
Figure 6 shows an analysis of the distribution of wall shear stress showed that the FAC method produced the lowest shear stress distribution at the ascending aorta breach. The maximum shear stress of the ascending aorta breach was 570 Pa. The maximum shear stress of the ascending aorta breach for AAC, IAC, and FAC was 393, 873, and 243 Pa, respectively. The maximum shear stress of the femoral artery breach was 715 Pa. The maximum shear stress of the femoral artery breach at AAC, IAC, and FAC was 1,128, 1,110, and 1,186 Pa, respectively.
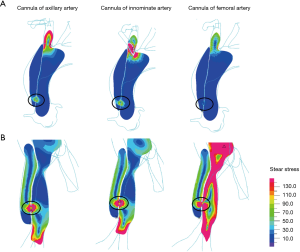
The result of the changes in wall shear stress distribution at the ascending aorta breach in condition B
Figure 7 showed that the FAC method produced the lowest shear stress distribution at the ascending aorta. The maximum shear stress of ascending aorta breach with AAC, IAC, and FAC was 67, 326, and 66 Pa, respectively. The maximum shear stress of femoral artery breach with AAC, IAC, and FAC was 334, 388, and 854 Pa, respectively.
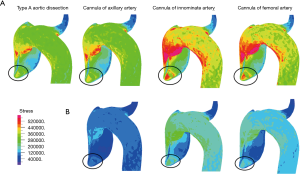
The result of the changes in wall stress distribution the false lumen at the ascending aorta breach
Figure 8 showed the stress changes in the false lumen, and found that AAC had the lowest stress change to the false lumen, while IAC had the highest stress in condition A. The maximum stress at rupture of the ascending aorta in TAAD was 0.64 MPa. The maximum stress at the rupture of the ascending aorta in AAC, IAC, and FAC was 0.67, 0.93, and 0.83 MPa, respectively. After the heart completely stopped blood supply in condition B, IAC was shown to have the highest level of stress and AAC was shown to have the lowest stress in the false lumen. The maximum stress at the rupture of the ascending aorta in AAC, IAC, and FAC was 0.17, 0.37, and 0.28 MPa, respectively. Compared with condition A, the velocity, shear stress, and stress of AAC and IAC were lower in condition B.
Discussion
The ideal cannulation strategy for TAAD should be easy to establish, minimize any organ malperfusion, prevent the progression of the intimal dissection flap or aortic rupture, and ensure the brain’s optimal protection other vital organs (21). Although different cannulation strategies were adopted based on the surgeon’s preference, skill, and patient’s anatomical characteristics, and none of the existing cannulation strategies was perfect and/or without complications, currently, there is controversy cannulation strategy in TAAD is optimal (6).
Due to a lack of visual monitoring methods in the CPB process, the advantages and disadvantages of cannulation have largely been determined by undertaking analyses of clinical prognostic outcomes. CFD (based on the CTA data of patients) can provide a visualization of blood flow analyses (22). The simulation model provides details of the flow and speed of each blood vessel branch when different cannulation strategies are applied, and also measures the stress and shear stress at different positions of the aortic wall. CFD can be used to guide cannulation strategies. Hillebrand et al. found that an unsuitable AAC site could lead to vertebral artery orifice by the cannula or a subclavian steal phenomenon based on the CFD technique (23). Numata et al. also found that right subclavian artery cannulation is cerebroprotective, especially on the right side via CFD (24). Based on the above similar studies, we also tried to use CFD to explain clinical problems, such as the hemodynamic difference between different arterial cannulations. In our previous study, central cannulation was found to provide the best-oxygenated flow and pressure to carotid arteries (CA), and AAC preferentially perfused the right CA at the expense of the left CA in the extracorporeal membrane oxygenation CFD model (25). In the present study, our CFD results demonstrated that both AAC and IAC significantly increased the blood flow of the axillary artery, innominate artery, and renal artery. However, compared with IAC and FAC, AAC provides the most blood flow to the brain in both conditions A and B (1,855.47 vs. 1,648.03 vs. 2,009.5 mL/min). This may be the reason can explain for ante-grade perfusion, such as IAC and AAC, is superior to FAC for cerebral protection.
Despite the risk of retrograde embolism, false lumen perfusion, and malperfusion, FAC is still an important clinical cannulation strategy in TAAD (26). Ram et al. found that both FAC and AAC have similar survival rates and significantly less renal impairment when using the femoral cannulation approach (5). Our data further confirmed that, compared with AAC and IAC, FAC showed the most significant improvement in renal blood flow (including left renal artery preoperative dissection involved in our case model). This also means that the FAC is conducive to lower body perfusion, and may help speed up cooling and re-healing. That could explain why is method is preferred by many surgeons.
Different cannulation modes have an effect on the flow velocity of the entry tear, but this effect is related to different states of CPB. In condition A, we simulated the heart and the CPB work together, and the volume was defined as CO 2.5 L/min and CPB 2.5 L/min according to clinical experience. We found that the velocity from AAC and IAC at the entry tear was higher than that from FAC. Furthermore, the velocity of entry tears significantly decreased in condition B, which equivalent to only CPB working (5.0 L/min) via cannula. The indicated that some blood will still enter the false lumen during partial CPB before cross-clamping the aorta and may be a potential factor causing the body’s insufficient perfusion due to increasing blood shunt. Unfortunately, this fractional flow cannot be measured with current technology. Shear stress and stress of entry tear also have similar trends. Although it is not clear what the consequences of this blood shunt is caused by, it may be beneficial for system perfusion by aortic cross-clamping as early as possible to reduce false lumen shunt perfusion. However, this needs further confirmation.
The changes in shear stress and stress of entry tear were related to blood damage and the further expansion of the false lumen (27). Therefore, we further analyzed the variation of these parameters on entry tear and exit tear in 2 conditions. Shear stress and stress under condition B were lower than those under condition A during AAC and IAC. Furthermore, AAC had lower shear stress and stress at the entry/exit tear than IAC. That is, AAC may have more advantages than IAC, especially in reducing stress and shear stress of tear.
Therefore, in this case model (the entry tear and the exit tear were located in the ascending aorta and the left iliac artery separately, and others major multiple communicating tears and/or secondary tears were not involved), although all three cannulation approaches were acceptable, AAC appeared to be superior to IAC, but FAC appeared to be superior for renal artery and lower limb perfusion.
Due to the limited space of the paper, this study only showed part of the research data, which only represents the changes of hydrodynamic parameters at the breach. The changes could occur in any part of the lumen, and these unknown changes need to be clarified in future studies.
We did not consider setting up a normal control model. This was because traditional open-heart surgery almost always involves an anterograde cannula of the ascending aorta. Comparisons and controversy between different cannulation sites would only exist in specific cases, such as TAAD.
Although the anatomy of TAAD was highly complex and more tears may have been included, this CFD model still represents a population of patients with 2 tears. Simplified the model was used and some branches of the celiac trunk were omitted (e.g., the celiac and superior mesenteric artery). Although this may not appear to be a perfect model and there may be numerical simulation bias, the purpose of the present study was to compare variations in fluid mechanical parameters under different cannulations model. Therefore, it had no direct interference with the results. It is worth noting that the total blood flow of the branch vessels was higher than that of the actual condition which was caused by this simplified model. In the future, we will further verify the hydromechanical differences in multiple tear models and the complex pathological characteristics in different patients.
Conclusions
Hemodynamic characteristics are different according to the cannulation modes used during different CPB states. The FSI model based on CFD could be used to clearly show these parameter changes and provide guidance for clinicians to design the optimal cannulation perfusion strategy according to different dissection characteristics.
Acknowledgments
Funding: The research was supported by the Science and Technology Project of Guangdong Province (Nos. 2016B090917001, 2017B090912006), Sanming Project of Medicine in Shenzhen (No. SZSM201612019), and Medical Scientific Research Foundation of Guangdong Province in China (No. A2021241).
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at http://dx.doi.org/10.21037/atm-21-605
Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-21-605
Conflict of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-21-605). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All procedures performed in this study involving human participants were in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by ethics board of Gaozhou Hospital (No. GYLLYJ-2020014) and informed consent was taken from the patient.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Evangelista A, Isselbacher EM, Bossone E, et al. Insights From the International Registry of Acute Aortic Dissection: A 20-Year Experience of Collaborative Clinical Research. Circulation 2018;137:1846-60. [Crossref] [PubMed]
- Suzuki T, Asai T, Kinoshita T. Emergency Surgery for Acute Type A Aortic Dissection in Octogenarians Without Patient Selection. Ann Thorac Surg 2019;107:1146-53. [Crossref] [PubMed]
- Kostadinovska B, Nikolic A, Slaveski D, et al. Acute aortic dissection in a patient with Marfan syndrome during advanced pregnancy. J Card Surg 2020;35:499-502. [Crossref] [PubMed]
- Gudbjartsson T, Ahlsson A, Geirsson A, et al. Acute type A aortic dissection - a review. Scand Cardiovasc J 2020;54:1-13. [Crossref] [PubMed]
- Ram E, Krupik Y, Lipey A, et al. Is Axillary Better Than Femoral Artery Cannulation in Repair of Acute Type A Aortic Dissection. Innovations (Phila) 2019;14:124-133. [Crossref] [PubMed]
- Abe T, Usui A. The cannulation strategy in surgery for acute type A dissection. Gen Thorac Cardiovasc Surg 2017;65:1-9. [Crossref] [PubMed]
- Schachner T, Nagiller J, Zimmer A, et al. Technical problems and complications of axillary artery cannulation. Eur J Cardiothorac Surg 2005;27:634-7. [Crossref] [PubMed]
- Augoustides JG, Desai ND, Szeto WY, et al. Innominate artery cannulation: the Toronto technique for antegrade cerebral perfusion in aortic arch reconstruction--a clinical trial opportunity for the International Aortic Arch Surgery Study Group. J Thorac Cardiovasc Surg 2014;148:2924-6. [Crossref] [PubMed]
- Garg V, Peterson MD, Chu MW, et al. Axillary versus innominate artery cannulation for antegrade cerebral perfusion in aortic surgery: design of the Aortic Surgery Cerebral Protection Evaluation (ACE) CardioLink-3 randomised trial. BMJ Open 2017;7:e014491 [Crossref] [PubMed]
- Harky A, Grafton-Clarke C, Hadlett M, et al. In thoracic aortic surgery, is innominate artery cannulation a safe and effective alternative to axillary artery cannulation. Interact Cardiovasc Thorac Surg 2019;29:604-7. [Crossref] [PubMed]
- Harky A, Wong C, Chan J, Zaki S, Froghi S, Bashir M. Innominate artery cannulation in aortic surgery: A systematic review. J Card Surg 2018;33:818-25. [Crossref] [PubMed]
- Di Eusanio M, Ciano M, Labriola G, et al. Cannulation of the innominate artery during surgery of the thoracic aorta: our experience in 55 patients. Eur J Cardiothorac Surg 2007;32:270-3. [Crossref] [PubMed]
- Houben IB, Patel HJ. Acute Type A Aortic Dissection: Managing More Than Just the Entry-Tear. Semin Thorac Cardiovasc Surg 2019;31:122-8. [Crossref] [PubMed]
- Osswald A, Karmonik C, Anderson JR, et al. Elevated Wall Shear Stress in Aortic Type B Dissection May Relate to Retrograde Aortic Type A Dissection: A Computational Fluid Dynamics Pilot Study. Eur J Vasc Endovasc Surg 2017;54:324-30. [Crossref] [PubMed]
- Ong CW, Wee I, Syn N, et al. Computational Fluid Dynamics Modeling of Hemodynamic Parameters in the Human Diseased Aorta: A Systematic Review. Ann Vasc Surg 2020;63:336-81. [Crossref] [PubMed]
- Costache VS, Yeung KK, Solomon C, et al. Aortic Remodeling After Total Endovascular Aortic Repair With Multilayer Stents: Computational Fluid Dynamics Analysis of Aortic Remodeling Over 3 Years of Follow-up. J Endovasc Ther 2018;25:760-4. [Crossref] [PubMed]
- Malvindi PG, Pasta S, Raffa GM, et al. Computational fluid dynamics of the ascending aorta before the onset of type A aortic dissection. Eur J Cardiothorac Surg 2017;51:597-9. [PubMed]
- Xu H, Piccinelli M, Leshnower BG, et al. Coupled Morphological-Hemodynamic Computational Analysis of Type B Aortic Dissection: A Longitudinal Study. Ann Biomed Eng 2018;46:927-39. [Crossref] [PubMed]
- Kreuzer M, Sames-Dolzer E, Schausberger L, et al. Double-arterial cannulation: a strategy for whole body perfusion during aortic arch reconstruction. Interact Cardiovasc Thorac Surg 2018;27:742-8. [Crossref] [PubMed]
- Gu K, Zhang Z, Gao B, et al. Hemodynamic effects of perfusion level of peripheral ECMO on cardiovascular system. Biomed Eng Online 2018;17:59. [Crossref] [PubMed]
- Tsiouris A, Elkinany S, Ziganshin BA, et al. Open Seldinger-Guided Femoral Artery Cannulation Technique for Thoracic Aortic Surgery. Ann Thorac Surg 2016;101:2231-5. [Crossref] [PubMed]
- Kaufmann TA, Hormes M, Laumen M, et al. The impact of aortic/subclavian outflow cannulation for cardiopulmonary bypass and cardiac support: a computational fluid dynamics study. Artif Organs 2009;33:727-32. [Crossref] [PubMed]
- Hillebrand J, Konerding MA, Koch M, et al. Anatomic and flow dynamic considerations for safe right axillary artery cannulation. J Thorac Cardiovasc Surg 2013;146:467-71. [Crossref] [PubMed]
- Numata S, Itatani K, Kawajiri H, et al. Computational fluid dynamics simulation of the right subclavian artery cannulation. J Thorac Cardiovasc Surg 2017;154:480-7. [Crossref] [PubMed]
- Gu K, Zhang Y, Gao B, et al. Hemodynamic Differences Between Central ECMO and Peripheral ECMO: A Primary CFD Study. Med Sci Monit 2016;22:717-26. [Crossref] [PubMed]
- Ayyash B, Tranquilli M, Elefteriades JA. Femoral artery cannulation for thoracic aortic surgery: safe under transesophageal echocardiographic control. J Thorac Cardiovasc Surg 2011;142:1478-81. [Crossref] [PubMed]
- Long Ko JK, Liu RW, Ma D, et al. Pulsatile hemodynamics in patient-specific thoracic aortic dissection models constructed from computed tomography angiography. J Xray Sci Technol 2017;25:233-45. [Crossref] [PubMed]
(English Language Editor: R. Scott)


