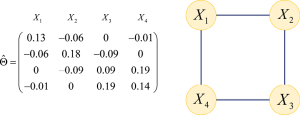
Application of graphical lasso in estimating network structure in gene set

Introduction: the importance of structure learning in gene set

Gene set analysis or pathway analysis tools play an important role in exploring the relationship between a group of genes and phenotypes of interest (1,2). How genes in this group work cooperatively to regulate or stimulate the complex biological function in different cellular status, however, often remains a mystery. Based on scientific studies or other text mining techniques (3,4), several public databases, such as KEGG (5), BioGRID (6) and STRING (7), have already annotated biological functions as pathways and the interactions within the molecular network. Therefore, it is possible to examine if the estimated correlation from the raw data is in conformity with the information retrieved from those public databases. Questions in the following may arise: “Can we directly estimate the interactions or learn the structure relationship among a group of genes only from the data?”; “Is there any statistical implementation that can help to answer this question?”

Answers to these questions may provide an opportunity for researchers to construct the gene network, and most importantly, to discover novel relationships within a group of genes (8-11). The graphical lasso (12) is a widely used approach in structure learning research as well as a useful tool to answer the above questions (13). It was proposed to estimate a sparse graph by utilizing the lasso penalty in the precision matrix of a multivariate normal distribution. Here we discuss how to estimate the network structure based on the multivariate normal distribution, and next introduce the rationale and the estimation procedure of the graphical lasso. Then, we demonstrate the graphical lasso algorithm with a real cancer application and conclude with a brief summary.

Structure learning with graphical lasso

Gene set analysis is often considered for microarray gene expression levels to investigate the association between a set of genes and a complex trait after a collection of differentially expressed genes have been identified (14-16). It is common to assume that the gene expression values in the gene set follow a multivariate normal distribution, also known as the Gaussian graphical model for gene network. This assumption is popular because of the theoretical statistical properties. For a group of P genes, assume the P– dimensional vector X follows a multivariate normal distribution,

$$X=(X_1,X_2,\mathrm{..},X_P)~MVN(\underset{˜}{\mu },\Sigma )$$[1]

Inside this vector, each component $X_i,i=1,2,\mathrm{..},P$ is a random variable representing the gene expression value of gene i. This distribution can be used to construct the network of these P genes. If a network follows this distribution, then the absence of an edge between two nodes (two random variables) implies that the two random variables are conditionally independent given all other variables. In fact, information of this conditional independence can be obtained from the precision matrix $\Theta$, where $\Theta ={\Sigma }^{-1}$, in this multivariate normal distribution $MVN(\underset{˜}{\mu },\Sigma )$ for X = (X₁,X₂,..,X_P). Specifically, if the (i,j) entry of $\Theta$ equals zero, it implies that X_i and X_j are conditionally independent. By assuming a multivariate normal distribution for the multi-dimensional gene expression values, the construction of the gene network structure can be based on the estimation of the precision matrix of the multivariate normal distribution. The mathematical proof and descriptions are detailed in (17).

The graphical lasso is a fast and efficient algorithm for estimating inverse covariance matrices (12,18). It is similar to the original lasso approach (19), but the graphical lasso focuses on selecting which edge to exist in a network rather than which variable to select in a regression problem. The graphical lasso adopts the convex optimization strategy to estimate the precision matrix by maximizing the following penalized log-likelihood

$$\log \det (\Theta )-trace(S\Theta )-\lambda {\Vert \Theta \Vert }_1$$[2]

where ${\Vert \Theta \Vert }_1={\displaystyle {\sum }_{j,k}\left|{\theta }_{jk}\right|}$ is the element-wise ${\mathcal{l}}_1$ norm of the precision matrix, S is the sample covariance matrix, and λ is the tuning parameter controlling the sparsity of the network. After obtaining the estimated precision matrix $\widehat{\Theta }$ from the graphical lasso algorithm, the network can be constructed based on the non-zero elements in $\widehat{\Theta }$. Figure 1 is a simple example for illustrating the equivalence between the estimated precision matrix and the corresponding network structure. Note that no edge appears between nodes X₁ and X₃ and between X₂ and X₄, since the corresponding two entries in $\widehat{\Theta }$ are zero.

Figure 1 A simple example for illustration.

Real data application: the lung cancer study

The expression data from a lung cancer study (20) is demonstrated here to show the utilization of the graphical lasso in estimating the network structure for a selected gene set. This data set was downloaded from the Gene Expression Omnibus (GEO, https://www.ncbi.nlm.nih.gov/geo/) and the corresponding accession number in NCBI data portal is “GSE19804”. This data set contains gene expression values extracted from 60 paired tumor and normal tissues. Forty-seven tumor tissue samples categorized as tumor stage 1 and 2 were selected into the following analysis. The STRING database (https://string-db.org/; Version 11.0) was considered to determine the gene set involving the protein-protein interaction (PPI) network of the EGFR gene. The EGFR gene was illustrated here because it has been shown in many studies that the EGFR gene is associated with tumor progression of lung cancer (21,22). In addition, several therapeutic drugs have already been developed to target on EGFR for lung cancer treatment (23-25). A novel interaction between these genes may help to unravel the underlying mechanism or improve therapeutic treatments for the cancer patients. The following analysis contained the gene expression values from 11 genes of the 47 tumor tissues. The expression value is the average probe log2 RMA signal intensity.

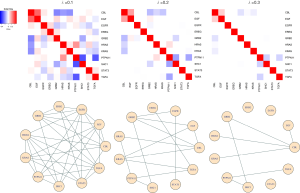
The analysis can be conducted with the function “glasso” in R package “glasso” (26). The input is the sample variance covariance matrix which can directly be calculated with the R basic function “var”, and the lambda tuning parameter can be assigned by the option “rho” in the “glasso” function. Figure 2 shows the resulting network structures constructed by the graphical lasso approach corresponding to different lambda tuning values. As we can see, when the lambda value increases, the degree of the sparsity in the network also increases. Some degree of sparsity in the network can reflect the underlying biological reality, and is often easier to interpret, particularly in the high-dimensional setting (27). Some edges in the estimated network, e.g., the connection between EGFR and GRB2, are consistent with the reports in (5) and (7). Furthermore, the results indicate that GRB2 and CBL contains more connections than others in the estimated graph, implying that these two genes and its immediate neighboring nodes may form a potential target for future lung cancer genetics research.

Figure 2 Estimated network structure of the 11 protein-protein interaction (PPI) genes of epidermal growth factor receptor (EGFR) with the graphical lasso. The upper panel contains heatmaps of the estimated precision matrices with different lambda values. The lower panel lists the corresponding graph structures. Note that if the entry in the estimated precision matrix is zero, then the corresponding paired nodes will not have a connecting edge between them in the network structure.

Brief summary

This report discusses the importance of structure learning in gene set analysis. The graphical lasso approach was introduced in constructing the network structure and a real data from a lung cancer study was considered to demonstrate the use of the graphical lasso. The main advantage of the graphical lasso is that it can reconstruct the network based on the raw data without incorporating other existing network profiles. By applying the graphical lasso in gene set analysis, we may discover a novel interaction between a set of genes and provide insight into the understanding of the complex biological mechanism.

Acknowledgments

Funding: This work was supported in part by the Taiwan Ministry of Science and Technology (MOST 109-2314-B-002-152).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-6490). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. de Leeuw CA, Neale BM, Heskes T, et al. The statistical properties of gene-set analysis. Nat Rev Genet 2016;17:353-64. [Crossref] [PubMed]
2. Khatri P, Sirota M, Butte AJ. Ten Years of Pathway Analysis: Current Approaches and Outstanding Challenges. PLoS Comput Biol 2012;8:e1002375. [Crossref] [PubMed]
3. Chen H, Sharp BM. Content-rich biological network constructed by mining PubMed abstracts. BMC Bioinformatics 2004;5:147. [Crossref] [PubMed]
4. Hsiao YW, Lu TP. Text-mining in cancer research may help identify effective treatments. Transl Lung Cancer Res 2019;8:S460-3. [Crossref] [PubMed]
5. Kanehisa M, Goto S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res 2000;28:27-30.
6. Oughtred R, Stark C, Breitkreutz BJ, et al. The BioGRID interaction database: 2019 update. Nucleic Acids Res 2019;47:D529-41. [Crossref] [PubMed]
7. Szklarczyk D, Gable AL, Lyon D, et al. STRING v11: protein-protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res 2019;47:D607-13. [Crossref] [PubMed]
8. Thompson D, Regev A, Roy S. Comparative Analysis of Gene Regulatory Networks: From Network Reconstruction to Evolution. Annu Rev Cell Dev Biol 2015;31:399-428. [Crossref] [PubMed]
9. Sun N, Zhao H. Reconstructing transcriptional regulatory networks through genomics data. Stat Methods Med Res 2009;18:595-617. [Crossref] [PubMed]
10. Ghanbari M, Lasserre J, Vingron M. Reconstruction of gene networks using prior knowledge. BMC Syst Biol 2015;9:84. [Crossref] [PubMed]
11. Juang JMJ, Lu TP, Lai LC, et al. Disease-Targeted Sequencing of Ion Channel Genes identifies de novo mutations in Patients with Non-Familial Brugada Syndrome. Sci Rep 2014;4:6733. [Crossref] [PubMed]
12. Friedman J, Hastie T, Tibshirani R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008;9:432-41. [Crossref] [PubMed]
13. Drton M, Maathuis MH. Structure Learning in Graphical Modeling. Annu Rev Stat Its Appl 2017;4:365-93. [Crossref]
14. Subramanian A, Tamayo P, Mootha VK, et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci 2005;102:15545-50. [Crossref] [PubMed]
15. Kim SY, Volsky DJ. PAGE: Parametric Analysis of Gene Set Enrichment. BMC Bioinformatics 2005;6:144. [Crossref] [PubMed]
16. Chang YH, Chiu YC, Hsu YC, et al. Applying gene set analysis to characterize the activities of immune cells in estrogen receptor positive breast cancer. Transl Cancer Res 2016;5:176-85. [Crossref]
17. Lauritzen SL. Graphical Models. Clarendon Press, 1996:314.
18. Witten DM, Friedman JH, Simon N. New Insights and Faster Computations for the Graphical Lasso. J Comput Graph Stat 2011;20:892-900. [Crossref]
19. Tibshirani R. Regression Shrinkage and Selection via the Lasso. J R Stat Soc Ser B Methodol 1996;58:267-88. [Crossref]
20. Lu TP, Tsai MH, Lee JM, et al. Identification of a Novel Biomarker, SEMA5A, for Non-Small Cell Lung Carcinoma in Nonsmoking Women. Cancer Epidemiol Biomarkers Prev 2010;19:2590-7. [Crossref] [PubMed]
21. Bethune G, Bethune D, Ridgway N, et al. Epidermal growth factor receptor (EGFR) in lung cancer: an overview and update. J Thorac Dis 2010;2:48-51. [PubMed]
22. Ciardiello F, Tortora G. EGFR Antagonists in Cancer Treatment. N Engl J Med 2008;358:1160-74. [Crossref] [PubMed]
23. Lu TP, Chuang EY, Chen JJ. Identification of reproducible gene expression signatures in lung adenocarcinoma. BMC Bioinformatics 2013;14:371. [Crossref] [PubMed]
24. Pao W, Chmielecki J. Rational, biologically based treatment of EGFR-mutant non-small-cell lung cancer. Nat Rev Cancer 2010;10:760-74. [Crossref] [PubMed]
25. Wang LB, Chuang EY, Lu TP. Identification of predictive biomarkers for ZD-6474 in lung cancer. Transl Cancer Res 2015;4:324-31.
26. Friedman J, Hastie T, Tibshirani R. glasso: Graphical Lasso: Estimation of Gaussian Graphical Models. 2019. R package version 1.11. Available online: https://CRAN.R-project.org/package=glasso
27. Ye J, Liu J. Sparse methods for biomedical data. SIGKDD Explor 2012;14:4-15. [Crossref] [PubMed]