Multiple imputation with multivariate imputation by chained equation (MICE) package
Introduction
“I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the seashore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.”—Isaac Newton.
Multiple imputation (MI) is an advanced method in handling missing values. In contrast to single imputation, MI creates a number of datasets (denoted by m) by imputing missing values. That is, one missing value in original dataset is replaced by m plausible imputed values. These values take imputation uncertainty into consideration. Statistics of interest are estimated from each dataset and then combined into a final one. While single imputation has been criticized for its bias (e.g., overestimation of precision) and ignorance of uncertainty about estimation of missing values, MI, if performed properly can give an accurate estimate of real result (1). However, MI is underutilized in medical literature due to lack of familiarity and computational challenges. To make clinicians become familiar to MI, the present article aims to provide a step-by-step tutorial to the use of R package to conduct MI for missing values. Before that, a brief description of basic ideas behind MI will be given.
Fundamentals of multiple imputation (MI)
MI procedure replaces each missing value with multiple possible values. Compared with single imputation, this procedure takes into account uncertainty behind missing value estimation. The procedure produces several datasets, from which parameters of interest can be estimated. For example, if you are interested in coefficient for a covariate in multivariable model, the coefficients will be estimated from each dataset resulting in m number of coefficients. Finally, these coefficients are combined to give an estimate of the coefficient, taking into account uncertainty in estimation of missing values. The variance of coefficient estimated in this way is less likely to be underestimated as compared to single imputation.
The imputation procedure carried out by first creating a prediction model for target variable with missing values from all other variables (Figure 1). In other words, the variable under imputation is the response variable and other relevant variables are independent variables. By default, predictive mean matching is used for continuous variables and logistic regression is used for dichotomous variable (2). Variables included into imputation are advised to be (I) predictive of missingness, (II) associated with the variable being imputed and (III) the outcome variable of your analysis (3,4).
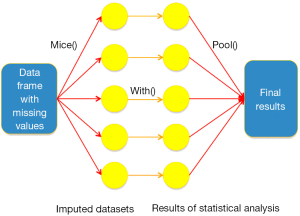
Working example
To establish a working example for illustration, I borrow the scenario from one of my recent research that investigated the relationship between lactate and mortality outcome (5). While the research was conducted by using MIMIC-II database involving >30,000 patients (6), the working example will artificially generate 150 patients with simulation. There are roughly 30% missing values in the lac variable.
Multiple imputation (MI) with multivariate imputation by chained equation (MICE) package
R provides several useful packages for MI. The commonly used packages include Amelia, MICE (7), and MI. In this article I will introduce how MICE works by using the simulated dataset.
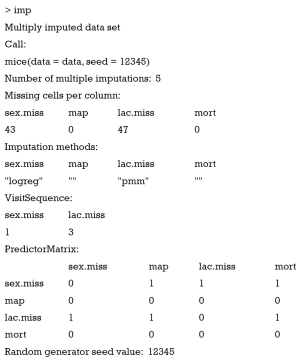
The first argument in mice() function is a data frame containing missing variables. I set a seed in the second place to make sure that readers can replicate the result. The result produced by mice() is stored in a list object imp which contains m imputed dataset, along with relevant information on how imputations are performed. You can take a look at the contents in imp.
In this call to function mice(), five datasets are imputed. There are 43 and 47 missing values in variables sex.miss and lac.miss, respectively. The imputation methods for dichotomous variable sex.miss is logistic regression and for continuous variable lac.miss is predictive mean matching. Visit sequence tells you the column order to impute data during one pass through the data. Visit sequence can be defined by the argument visitSequence =(1:ncol(data))[apply(is.na(data), 2, any). In the working example, sex.miss is first imputed, followed by lac.miss. Predictor matrix contains 0/1 data specifying which variables are used to predict target variable. Rows indicates target variable (variable to be imputed). A value “1” means that the column variable is used to predict row variable. For instance, the first row indicates that column variables map, lac.miss and mort are used to predict sex.miss. No variable is used to predict map and mort because both of them contain no missing value. You can choose any set of variables used for prediction by specifying the predictorMatrix =(1-diag(1, ncol(data))) argument. If you do not want to use mort to predict sex.miss, change the predictor matrix as follows:
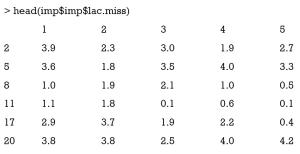
Imputations for a particular variable can be viewed in the following way. I use the head() function to save space (otherwise there will be 47 rows).
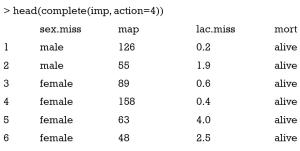
In this matrix you can have a look at what mice() has imputed in each imputation. Recall that you have not specified the number of imputations and the default is 5. The first row indicates the row number of missing values in original dataset. If the matrix contains negative values, you may need to review the imputation method. You can also view each of the five complete dataset by following code. Again head() is used to save space. The argument action=4 specifies that the forth imputation is visited.
Statistical analysis after imputation
Now that you have five complete datasets at hand, conventional statistical analysis can be performed. In observational studies, the first step is usually to perform univariate analysis to find out which variable is associated with outcome of interest. The following example illustrates how to perform t test and multivariable regression analysis.
The generic form of with() function is with(data, expr). It allows an R expression to be executed in an environment from data. The assignments within expression take place within data environment instead of the user’s workplace. In our example, the t.test() function takes place within imputed complete datasets contained in the object imp. Otherwise, if with() is not called the t.test() will use original incomplete dataset existing in the workplace. The above output only displays analysis of the first imputed dataset and other four are omitted to save space.
Nest I want to find out variables associated with mortality outcome by using logistic regression model. Note that logistic regression model is specified glm() function.
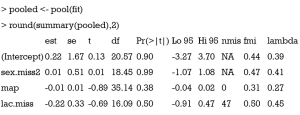
Now the list object fit contains results from five logistic regression analyses (note that there are five sets of logistic regression, and here I showed analysis from the first imputed dataset) and relevant information. In the first estimation, the coefficient for lac.miss is −0.33 for each one unit increase in lac.miss. Note there is a “2” behind sex.miss, which indicates level 1 is used as reference (recall that R treats sex.miss as factor variable). This is not the end of the story and you need to combine the five sets of results into one.
The pool() function is shipped with MICE package. It combines the results of m imputed complete data analysis. The variance is computed by taking into account the uncertainty in missing value imputation.
Summary
This article introduces how to perform MI by using MICE package. The idea of MI is to take into account uncertainty in predicting missing values by creating multiple complete datasets. There are varieties of imputation methods and users can choose the most appropriate one. In practice, the default setting is usually satisfactory. The with() function sets the environment for the expression to be performed, and the argument for the environment is the imputed datasets. Varieties of expressions can be executed including univariate analysis and multivariable regression models. Next, the pool() function is employed to combine results from analysis of each imputed datasets. The variance obtained from pool() function takes uncertainty of missing values into account.
Acknowledgements
None.
Footnote
Conflicts of Interest: The author has no conflicts of interest to declare.
References
- Donders AR, van der Heijden GJ, Stijnen T, et al. Review: a gentle introduction to imputation of missing values. J Clin Epidemiol 2006;59:1087-91. [PubMed]
- Morris TP, White IR, Royston P. Tuning multiple imputation by predictive mean matching and local residual draws. BMC Med Res Methodol 2014;14:75. [PubMed]
- White IR, Royston P, Wood AM. Multiple imputation using chained equations: Issues and guidance for practice. Stat Med 2011;30:377-99. [PubMed]
- Moons KG, Donders RA, Stijnen T, et al. Using the outcome for imputation of missing predictor values was preferred. J Clin Epidemiol 2006;59:1092-101. [PubMed]
- Zhang Z, Chen K, Ni H, et al. Predictive value of lactate in unselected critically ill patients: an analysis using fractional polynomials. J Thorac Dis 2014;6:995-1003. [PubMed]
- Zhang Z. Accessing critical care big data: a step by step approach. J Thorac Dis 2015;7:238-42. [PubMed]
- Buuren SV, Groothuis-Oudshoorn K. mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software 2011;45:1-67.