Determining the frequency of sporadic cases of rare X-linked disorders
Introduction
CC Li gives the widely-accepted version of the balance between mutation and selection for sex-linked genes (1). On page 510 he gives the estimate of the mutation rate for haemophilia as μ=0.00002=20×10−6, which he attributes to Haldane [1935] (2). Clearly Haldane regarded this contribution to population genetics as important because it recurs with variations in several of his publications. In brief, in our notation, Li gives the identity

where μ is the rate of mutation from the normal to the haemophilia allele, f is the survival value, or fitness, of haemophilic males and g is the frequency of the recessive allele for haemophilia. Li gives a brief heuristic justification for the formula connecting mutation rate, fitness and gene frequency.
Haldane [1938] gives the following verbal justification for the formula (3): if new genes for haemophilia can only appear in the X chromosome by mutation, this estimate of the frequency (once in 50,000 generations) follows from the fact that haemophilic males rarely live long enough to breed. And as about one third of the genes for haemophilia in the X chromosome are carried by males, the frequency of the gene in the X chromosome must be reduced by about one third in each generation, if it is not kept constant by new genes arising by mutation or some other process.
Haldane gave a series of lectures in the University of Gröningen, Holland, in March 1940. These lectures led to the publication of his monograph New Paths in Genetics (4). In it he says: “Now mutation, as in this case [haemophilia], increases the number of harmful genes in the population, whilst selection lowers it. If mutation and selection go on at steady rates, and the breeding system of the population does not alter, they will come into equilibrium, as I pointed out in 1927.” (5). He then explains the derivation of the formula given by Li.
Haldane [1948] writing “in the case of haemophilia”: ..“if x be the frequency in males at birth, f the fitness, and μ the mutation rate, 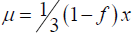 ”. Estimating f to be 0.286, Haldane calculated μ =3.16×10−5 (6).
”. Estimating f to be 0.286, Haldane calculated μ =3.16×10−5 (6).
Fraser [1972] examined “the possible long-term effects from the point of view of disease incidence in males and heterozygote prevalence in females of selective abortion as practiced in the case of X-linked deleterious conditions.” (7). He set out the following equilibrium conditions:
- The mutation rate m is equal in male and female germ cells;
- x0 is the initial incidence of affected males at birth and their relative fertility is f (<1);
- y0 is the initial prevalence of heterozygous females.
In the next generation:

and

At equilibrium, y1=y0 and x1=x0.
Fraser asserts that x0 =3m/(1−f) and y0 =[2m(2+f)]/(1−f). Further, when f=0 as in the case of a severe form of muscular dystrophy, these equilibrium conditions reduce to x0=3m and y0=4m.
We see here that the details of Fraser’s analysis are close to those of Haldane, but without acknowledgement. Fraser made detailed calculations for various strategies of selective abortion in the case of deleterious sex-linked conditions. He concluded, inter alia, that “under most strategies a marked reduction in the incidence of affected males occurs, in some cases at the cost of a very modest increase in the prevalence of female heterozygotes which should not give rise to concern.”
Haldane [1956] considered specifically the “sex-linked recessive muscular dystrophy of the Duchenne type” in the following way (8): let μ be the mutation rate per locus per generation in females, ν be the mutation rate per locus per generation in males, p be the frequency of heterozygous females, q be the frequency of affected males (among all births), x = μ/2μ + ν.
Then assuming complete male lethality, and normal segregation, we expect, in the next generation
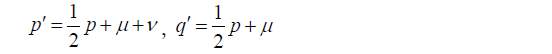
So at equilibrium

The equilibrium is quickly reached if μ and ν remain constant. At equilibrium the frequency of affected males whose condition is due to the heterozygosity of their mothers is μ+ν, the frequency of affected males whose condition is due to mutation in a maternal nucleus is μ. If a woman is heterozygous, half of her sons are expected to be affected. A mutation at an early stage in her embryonic life might render all her oogonia heterozygous. But most mutations occurring at nuclear divisions in her germ line would only affect a small fraction of her offspring. And if the future ova are all formed before birth, as is commonly believed, radiation or any other cause whose effect is cumulative through maternal life would only affect single ova. Neither of these statements is true for males. We are therefore, I think, justified in assuming that a fraction μ/2μ + ν, or x, of all affected males, will be sporadic cases.
We see from the above that Haldane has introduced separate mutation rates for eggs and sperm.
Stark uses an argument with some similarity to that of Haldane for Duchenne muscular dystrophy (9). However, as explained in the section on population genetics, it was defective in that it omitted a term in one of the equations. In this paper we take a further step for a rare recessive disorder in making provision for family planning and some reproductive potential for the affected male.
In the Discussion we note an adverse comment on Haldane and give some references to the Lesch-Nyhan syndrome.
Population genetics
The following is a deterministic model which attempts to relate the incidence of the disorder, such as haemophilia, to the mutation rate in eggs, denoted by μE, and sperm μS. Denote the frequency of the ‘normal’ gene in the population by q, so that the frequency of the gene on the X-chromosome which causes the disorder in boys is 1–q. Assume that the frequency of normal homozygous females is x = q2 and that of carrier females is h = 2q(1–q). We denote the frequency of normal males by y = q.
Assuming discrete, non-overlapping generations, the incidence of the disorder in boys is

where r is the proportion of carrier females identified as carriers who refrain from reproducing sons.
In the following generation, the frequencies are

and
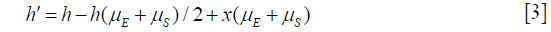
Note that x(μE + μS) was wrongfully omitted from the expression corresponding to Eq. [3] in the previous paper.
In this generation the frequency of the normal gene in females is

and in (normal) males is

where d' is an updated estimate of the incidence of the disorder in males and f is the fitness of males bearing the abnormal gene. Here f is taken as the proportion of affected males contributing to the gene pool of the following generation.
We define the frequency of the normal gene in the population as

Assuming values of r, f, μE and μS, we use the above formulae to generate a sequence of generations, including, in particular, the incidence of the disorder. After several generations the equilibrium gene frequency is reached, together with the incidence of the disorder from Eq. [1].
The equilibrium frequency of the abnormal gene is approximately

and the incidence of the disorder is

So the proportion of the cases arising from non-carrier mothers is μE / d.
Correcting the term, noted above, shows that when f =0 and r =0, the frequency of the abnormal gene is μE + 2μS and the incidence of the disorder is d = g + μE = 2(μE + μS) There is a difference in detail between this result and that given by Haldane as reproduced in the Introduction.
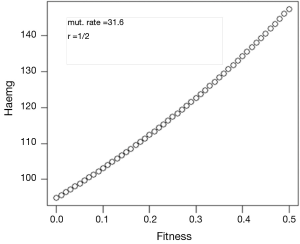
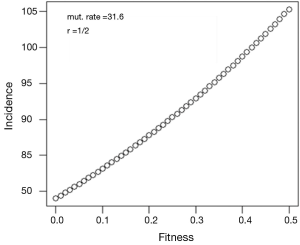
The possible use of formulae Eq. [7] and Eq. [8] is illustrated in Figures 1,2. In these, using Haldane’s estimate of the mutation rate for haemophilia, the same in eggs and sperm, values of d and g are depicted for the case r = ½, for f in the interval from zero to ½ (Figures 1,2).
Discussion
An international conference on human genetics was held in Calcutta, India in December 1992 to celebrate the centenary of Haldane’s birth. The contributions of the various speakers were published as a centennial tribute. The resulting papers were general laudatory with the exception of that by Ewens who was the only author to refer, briefly, to the subject of this paper (10). In the broader context of evolutionary genetics, Ewens writes: “A similar conclusion (to autosomal recessive) holds for a sex-linked trait such as haemophilia, where the frequency of haemophiliacs in the population is shown, by a similar calculation, again to be of order u (the mutation rate). Haldane then drew the conclusion that u is of order 10−5 to 10−4, presumably because this is approximately the frequency of haemophiliacs in the general population. But many difficulties are swept under the carpet..I detect a far from decisive analysis of the value of theoretical evolutionary population genetics in estimating mutation rates in Haldane’s <
Some of the things “swept under the carpet” are the reliability of the estimates of the incidence of haemophilia, whether sample sizes are adequate, and whether any population is in equilibrium. However various human geneticists have taken seriously Haldane’s publications in this area. Our purpose here is to suggest that the formulae given in the previous section may be useful in considering the public health implications of mutation, genetic analysis and counselling.
In the Introduction, we touch on the paper of Fraser who examined the possible long-term effects of selective abortion in the case of X-linked deleterious conditions. In a Festschrift to honour the work of George Robert Fraser, Ewens writes: “Fraser considered load arguments in much of his work on diseases relevant to man. These centred mainly on the mutational load..” (11). Ewens was concerned mainly with the controversies about genetic load and the cost of natural selection which had developed out of Haldane’s work on these concepts. As noted above, Ewens was highly critical of Haldane. However, Ewens does not criticise Fraser who used essentially the same arguments in making his basic calculations.
Francke et al. discuss the occurrence of new mutants in X-linked recessive Lesch-Nyhan disease (12). They note that the mutation rate for such genes “has generally been estimated according to the method of Haldane” [1935]. They state that according to the theory of Haldane given at the beginning of this paper, it is expected that one-third of all affected males per generation would represent new mutations. They found an unexpectedly low number of homozygous normal mothers—most patients in their sample were found to have mothers carrying the gene. Morton and Lalouel questioned the validity of their methods (13) and received a rebuttal (14).
In the case of Lesch-Nyhan syndrome, Torres et al. note that carrier diagnosis can be done by genomic DNA sequencing of the HPRT1 gene fragment where the mutation is found in the family propositus. Prenatal diagnosis can be performed with amniotic cells obtained by amniocentesis (15).
It is beyond the scope of this paper to go into all the difficulties which have come to light. We leave it to the reader to judge whether the model presented in the second section is of value. It does at least permit some simple calculations, going beyond Haldane’s, to explore the possible effects of new medical technologies.
Acknowledgements
None.
Footnote
Conflicts of Interest: The author has no conflicts of interest to declare.
References
- Li CC. First Course in Population Genetics. Pacific Grove CA: The Boxwood Press; 1976.
- Haldane JB. The rate of spontaneous mutation of a human gene. 1935. J Genet 2004;83:235-44. [PubMed]
- Haldane JB. The location of the gene for haemophilia. Genetica 1938;20:423-30.
- Haldane JB. New Paths in Genetics. New York: Harper & Brothers, 1942.
- Haldane JB. A Mathematical Theory of Natural and Artificial Selection Part X. Some Theorems on Artificial Selection. Genetics 1934;19:412-29. [PubMed]
- Haldane JB. The rate of mutation of human genes. Proceedings of the Eighth International Congress of Genetics 1948;35:267-73.
- Fraser GR. Selective abortion, gametic selection, and the X chromosome. Am J Hum Genet 1972;24:359-70. [PubMed]
- Haldane JB. Mutation in the sex-linked recessive type of muscular dystrophy; a possible sex difference. Ann Hum Genet 1956;20:344-7. [PubMed]
- Stark AE. Determinants of the incidence of Duchenne muscular dystrophy. Ann Transl Med 2015;3:287. [PubMed]
- Ewens WJ. Beanbag Genetics and After. In: Majumder PP, editors. Human Population Genetics: A Centennial Tribute to J. B. S. Haldane. New York: Springer US, 1993:7-29.
- Ewens WJ. Fraser and the genetic load. In: Mayo O, Leach CR, editors. Fifty Years of Human Genetics: a Festschrift and liber amicorum to celebrate the life and work of George Robert Fraser. Kent Town: Wakefield Press, 2007;402-8.
- Francke U, Felsenstein J, Gartler SM, et al. The occurrence of new mutants in the X-linked recessive Lesch-Nyhan disease. Am J Hum Genet 1976;28:123-37. [PubMed]
- Morton NE, Lalouel JM. Genetic epidemiology of Lesch-Nyhan disease. Am J Hum Genet 1977;29:304-11. [PubMed]
- Francke U, Felsenstein J, Gartler SM, et al. Answer to criticism of Morton and Lalouel. Am J Hum Genet 1977;29:307-11. [PubMed]
- Torres RJ, Puig JG, Ceballos-Picot I. Clinical utility gene card for: Lesch-Nyhan syndrome--update 2013. Eur J Hum Genet 2013.21. [PubMed]