
A novel parametric method-based nomogram of left ventricular internal diameters in normal Chinese adults
Introduction
The normal reference ranges of cardiac structures in adults are largely reported in various guidelines along with the corresponding studies (1-7). In most studies, the reference values are obtained by two approaches. The first is to establish cut-off values for defining mild, moderate, and severe abnormalities based on standard deviations (SDs) that deviate from the reference limit empirically. The other is to explore abnormalities based on percentile values (e.g., 95th, 99th) of cardiac measurements derived from a population that includes both healthy people and those with disease. The advantages and disadvantages of both methods are obvious, and only the sex-, age- and body surface area (BSA)-normalized normal reference values are deemed appropriate (1). Most studies and guidelines assume that the BSA is linearly correlated with left ventricular structure measurements with a zero intercept, especially in adults (1-7), but this was proven to be incorrect by various lines of physiologic and mathematical evidence (8-13). One possible explanation is that diameters, areas, and volumes have nonlinear relationships with each other, so these structure parameters cannot all have isometric relations with BSA (13).
The Z-score is a standard statistic value that demonstrates how many SDs a value deviates from the mean in a normally distributed population. For example, an observed measurement that is 2 SDs above the mean, corresponding to 97.7th percentile, has a Z-score of 2, and a measurement 2 SDs below the mean, corresponding to the 2.3rd percentile, has a Z-score of −2. Such a parametric statistical value provides a better way than simply defining “normal or abnormal values”, by allowing clinicians to appreciate the magnitude of the abnormality. A chamber size is defined as normal at a Z-score of −2 to 2, mild at a Z-score of ±2 to ±3, moderate at a Z-score of ±3 to ±4, and severe at a Z-score >4 or a Z-score <−4 according to the 2015 Western adult guideline (1).
Our study aims to mathematically explore the correlations between the left ventricular internal diameters and BSA in healthy Han Chinese adults and to provide normative data with corresponding Z-scores. We present the following article in accordance with the STROBE reporting checklist (available at http://dx.doi.org/10.21037/atm-20-2195).
Methods
Study population
This is a prospective, observational, multicentre study. A total of 602 healthy Han Chinese adult volunteers were screened at the First Affiliated Hospital of Nanjing Medical University (n=206), the Ninth People’s Hospital of Suzhou (n=194) and Sir Run Run Hospital Affiliated Nanjing Medical University (n=202), Jiangsu, China, over a 9-month period (2018-7-1 to 2019-3-31). Inclusion criteria, in brief, were age 18 to 79 years with normal cardiac physical examinations and with normal laboratory tests, including glycaemia, cholesterol, and renal function, obtained within 3 months before the study. Exclusion criteria were a medical history of structural cardiac disease or systemic diseases known to influence the cardiac structure, a history of chronic alcoholism, current cardioactive drug therapy, poor image quality on echocardiography, pregnancy, and severe obesity (body mass index ≥35 kg/m2). Parameters of height, weight, and blood pressure were measured and recorded with clinical screenings. The BSA was then computed with Haycock’s formula (14). The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The protocol was approved by the ethics committee of the First Affiliated Hospital of Nanjing Medical University (approval ID: 2020-SR-255) and informed consent was taken from all the patients.
Echocardiographic measurement
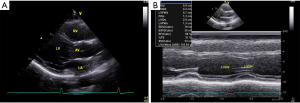
All enrolled participants underwent a comprehensive two-dimensional guided M-mode echocardiographic examination with a commercially available ultrasound system (Sonos 5500 or 7500, Philips Medical Systems, Andover, MA). All subjects were examined according to a predefined protocol: (I) the technique of grey-scale second-harmonic imaging was adopted with the appropriate frequency, depth, image contrast, sector size and LV border visualization; (II) images were acquired during a breath-hold at end-expiration for the minimum of cardiac respiratory motion, and at least three cardiac cycles were recorded for analysis; (III) the subjects were in left lateral position; (IV) the left ventricular internal diameter was measured by two-dimensional guided M-mode echocardiography (sweep speeds of 100–200 mm/s) from the parasternal long-axis view, as the guidelines recommended; (V) the parameters were carefully assessed at or immediately below the level of the mitral valve leaflet tips with the leading-edge to leading-edge technique.
Data collection and statistical analysis
Two-dimensional guided echocardiography was carried out in each centre according to the above protocol. Data were recorded and stored in the digital raw-data DICOM format and transferred to the First Affiliated Hospital of Nanjing Medical University for analysis and quality control. To minimize the effects of age differences, we divided the subjects into 3 age groups: 18–39, 40–59 and 60–79 years. Data are presented as mean ± SD. For categorical variables, counts and percentages are presented. Differences between sexes were analysed with the unpaired t-test. Age differences were compared with one-way ANOVA.
In this study, BSA was investigated as an independent variable affecting LViD. Correlations between BSA and LViD were tested by Pearson’s correlation test. Intra-observer and inter-observer variability were assessed in 30 randomly selected participants. The intra-class correlation coefficient (ICC) with its 95% confidence interval is reported. Regression analysis was performed on LViD plotted against BSA. A linear and several nonlinear models, including power, logarithmic, exponential, and polynomial (linear, quadratic, and cubic) models, were tested, and the best-fit model was chosen in accordance with the Akaike information criterion. The coefficient of determination (R2) was used to find the best-fit regression model. Once the best-fit model was identified, Z-score boundaries and nomograms of left ventricular diameter were calculated. For residual analysis, heteroscedasticity was assessed by the Breusch–Pagan test, and the Shapiro-Wilk test was adopted to test the normality of residuals. Autocorrelation was evaluated with the Durbin-Watson test. Studentized error residuals were utilized to exclude outliers from the analysis. A two-tailed P value of less than 0.05 was regarded as statistically significant. The data were analysed by SPSS version 22.0 (SPSS, IL, USA).
Results
General characteristics
This is a prospective, observational, multicentre study. A total of 602 subjects were screened at 3 medical centres during the 9-month study period. Twenty-five subjects were excluded for poor image quality or cardiac pathological status as detected by echocardiography. The remaining 577 subjects (43.3% male) were finally enrolled, with a mean age of 44.4±13.0 years. The demographic and echocardiographic characteristics of the eligible subjects are summarized in Table 1. The BSA (m2) was computed with the Haycock formula [14]: 0242653×weight (kg)0.5378×height (cm)0.3964. All enrolled subjects underwent two-dimensional guided M-mode echocardiography to measure the left ventricular end-diastolic diameter (LVDd) and left ventricular end-systolic diameter (LVDs) (Figure 1).
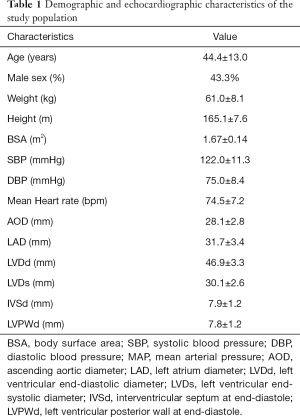
Full table
Regression analysis and Z-score calculations
Obvious correlations between BSA and both LVDd and LVDs were detected from Pearson’s correlation test, with coefficients of 0.781 and 0.734, respectively (P<0.001). A clear sex difference in both LVDd and LVDs was detected with the unpaired t-test (P<0.001 for both). However, no apparent difference between age intervals was found in LVDd (P=0.877) or LVDs (P=0.766) by one-way ANOVA. Sex- and age-specific differences are summarized in Table 2.

Full table
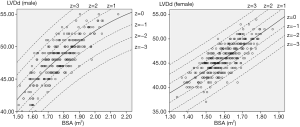
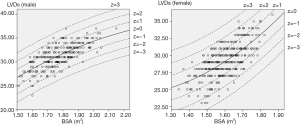
For each measurement, one linear and 7 nonlinear models (polynomial, compound, growth, logarithmic, exponential, inverse, power) are provided together with the estimated regression coefficients (β0, β1, β2), standard error (SE) and the coefficient of determination (R2). R2 is a statistical value commonly adopted to describe how well data fit a selected regression model (best fit). It has a range of 0 to 1. An R2 of 1 represents a perfect fit, and an R2 of 0 represents a total lack of fit. After the comparison of different regression models, the polynomial (quadratic) model was chosen as the best-fit model, with R2 values of 0.615 and 0.540 for the correlation of LVDd and LVDs, respectively, with BSA. Table 3 shows the regression results for LVDd and LVDs against BSA corrected by age and sex. Figures 2-7 show the overall and age-specific, sex-specific nomograms of LVDd and LVDs plotted against BSA. The superimposed solid line represents the estimated regression equation (labelled z=0). The dashed lines depicted in the nomograms represent the Z-scores of ±1, ±2, and ±3, which tell how many SEs above or below the regression line a measurement was.
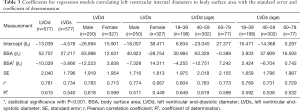
Full table
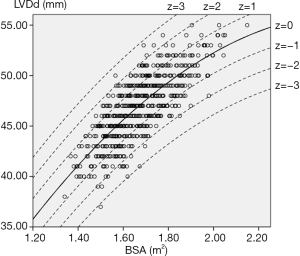
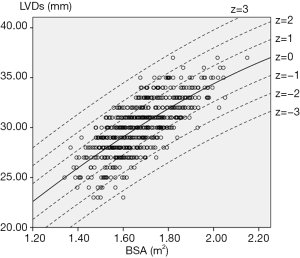


To calculate the Z-score for observed measurements by using our results, one can use the given polynomial model of Expected y=β0+β1×BSA+β2×BSA2 summarized in Table 3 to calculate the Z-score directly with the standard formula [Observed y −Expected y]/SE. Expected y means the expected measurement (LVDd or LVDs), which is calculated by the best-fit regression model, and SE means the standard error of the selected model. For example, to calculate the Z-score of a patient with a BSA of 1.8 m2 and an observed LVDd of 55 mm, the first step is to find the corresponding regression coefficients from Table 3 for LVDd, which are β0=−13.039, β1=52.707, β2=−10.029, and SE =2.040, then plugging these values into the formula to obtain the mean LVDd for BSA =1.8 m2.
[1]
[2]
Residual analysis and reproducibility
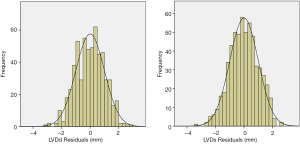
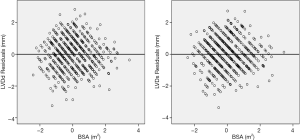
To ensure that no important bias was introduced by the regression models, residual analysis was performed. First, we assessed the distribution of the residual values with the Shapiro-Wilk test, which showed the normal distribution of the residuals in both LVDd (P=0.068) and LVDs equations (P=0.163). Then autocorrelation was evaluated by the Durbin-Watson test in both regression models, which yielded values of 1.612 and 1.516 for LVDd and LVDs, respectively, which meant that the residuals and BSA were isolated. Figures 8 and 9 show the plot of residuals according to BSA for the models of LVDd and LVDs, respectively. The dispersion in each graph appears symmetrical around the midline, which suggests the absence of heteroscedasticity. For further confirmation, the Breusch-Pagan test was run on both models. It yielded P values of 0.231 in LVDd and 0.0935 in LVDs, which confirmed that no obvious heteroscedasticity was detected in either regression model. Finally, we assessed the intra-observer and inter-observer reproducibility of LVDd and LVDs measurements, which showed good to excellent reproducibility, with an intraclass correlation coefficient (ICC) of 0.82 to 0.95 (Table 4).

Full table
Discussion
Main findings
BSA-specific reference values of LViD from regression analysis, with the corresponding Z-scores, are presented in this study. Polynomial (quadratic) regression equations were determined to be the best-fit models for both LVDd and LVDs. The results show that the upper and lower reference limits were higher in men than in women. However, no obvious difference was observed among different age intervals. To acquire more precise regression models, BSA/age-specific or BSA/sex-specific reference models are described in subgroups shown in Table 3, and residual analysis was performed to evaluate the bias of each formula. In consideration of the small sample size, BSA age- and sex-specific reference values were abandoned in this study.
Compared with paediatric R2 values (15-19), the relatively low R2 (0.45–0.65) of the best-fit regression models might be attributed to the following: First, the small sample of this study could have induced bias in the data distributions, particularly in the subgroup aged 60–79 years, as shown in Figures 6 and 7. Second, the continuous variable BSA was distributed in a narrow range in this study (1.34–2.15 m2), and the absence of small or large BSA values might have affected the goodness of fit. Furthermore, besides growth factors, complex pathologic or physiologic factors in adults could influence the cardiac structures or even BSA, especially in the elderly, which could have impacted the goodness of fit.
Left ventricular size and normative data
Measuring cardiac structures with a precise approach is crucial in the diagnosis and management of various structural heart diseases. Currently, the normative values and nomograms of echocardiography in adults are derived from various guidelines according to various databases (1-7). The most recent and convincing is the “Cardiac Chamber Quantification Recommendations” from the Eur Heart J Cardiovasc Imaging [2015] (1), in which the normal reference ranges of left ventricular size were derived from 7 large databases (3-7). Although BSA-normalized reference ranges and nomograms were presented in the recommendations, the use of isometric correction of BSA with LViD could contribute to a bias, as we mentioned above. Ethnicity is an important factor affecting cardiac structures, but the recommendation only provided the reference values of the white and black races and not Asian races. In China, the most recent guideline for adults referred to in clinical practice is the guideline from the Chinese Journal of Ultrasonography (2). The database behind the guideline was built from 1,394 healthy adult participants of 43 hospitals across the country. Compared with the recommendation of EHJ, the guideline of China only offered the normal reference ranges adjusted by age and sex, without BSA corrections, although the BSA-normalized concept was mentioned in the text. Most recently, Cantinotti et al. (20) critically reviewed adult echocardiographic nomograms and demonstrated that nearly all echocardiographic normative data in adults have been generally expressed as the mean values normalized by sex and age or indexed by BSA, instead of computing models with different variables to calculate Z-scores. Therefore, this study may offer a new perspective for calculating normal reference values. Regarding the sex differences, most guidelines and databases suggest that the size of the left ventricle is larger in men than in women, which is in accordance with our results. However, there is no clear consensus about the difference in LViD with age in adults (1-7).
To our knowledge, most published data with regression models to compute the Z-scores of various heart structures originated from studies conducted in the West (15-19). Only a few studies were conducted in developing countries, and all these data were mainly based on paediatric populations (21,22). The calculation of Z-scores has been widely used to normalize paediatric cardiac parameters in two-dimensional echocardiography, three-dimensional echocardiography and even cardiovascular magnetic resonance (23,24). However, not all cardiac parameters show good coefficients of determination for computing Z-scores, such as echocardiographic strain (ε) (25). In recent years, the concept of the Z-score has already been used to diagnose certain cardiovascular diseases (e.g., dilated cardiomyopathy) in adults (26). Therefore, establishing normative data by the calculation of the Z-scores is inevitable. Various regression equations have been used to correlate the left ventricle measurements with body size, and the most commonly adopted models are exponential and polynomial models. Some studies suggest that the exponential formula of the form Y = a ×BSAb + c provides the best correlation with all cardiac measurements with the minimal residual variance (13,27). However, these suggestions were mostly derived from paediatric populations. In adults, the change in cardiac structures with age and with BSA tends to be stable (28). Thus, a steep regression model might not be appropriate.
Many studies have used logarithmic transformation of the dependent variable to adjust for nonlinearity and to reduce model heteroscedasticity, but some potential bias could be introduced by such a transformation (29,30). First, logarithmic transforming may mask potentially strong outliers. Second, most cardiac structural parameters are normally distributed in any age group and in either sex, and in order to obtain optimal regression models, corresponding residual values must be normally distributed. However, the logarithmic transformation might contribute to the failure to produce normally distributed residual values by parametric normalization.
Study limitations
Our study has the following limitations. First, the study results mainly pertain to Han Chinese individuals, so they might not be generalizable to other ethnic populations. Second, a larger sample size would have allowed us to obtain better models with more variables to be normalized simultaneously (e.g., blood pressure, heart rate). Third, in elderly subjects, complicated pathologic or physiologic factors, such as kyphosis or height decline (31), may add potential bias by disturbing the body size calculation. Furthermore, we focused more on the structures rather than on their clinical functional status.
Conclusions
This study proposed a more comprehensive and precise approach for calculating normal reference values of left ventricular internal diameters with echocardiographic nomograms in healthy Han Chinese adults. Further studies with larger sample sizes are required to reinforce these data and to assess other cardiac structure parameters.
Acknowledgments
The authors would like to thank Dr. Li Chen from Sir Run Run Hospital Affiliated Nanjing Medical University for echocardiography measurements and Dookun M. Nabeel from the First Affiliated Hospital, Nanjing Medical University, for data collection.
Funding: None.
Footnote
Reporting Checklist: The authors have completed the STROBE reporting checklist. Available at http://dx.doi.org/10.21037/atm-20-2195
Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-2195
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-2195). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work (including full data access, the integrity of the data and the accuracy of the data analysis) in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study protocol adheres to the 1964 Helsinki Declaration and its successive emendations and was approved by the local ethics committee (approval ID: 2020-SR-255). Written informed consent was obtained from the patient for publication of this study and any accompanying images.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Lang RM, Badano LP, Mor-Avi V, et al. Recommendations for Cardiac Chamber Quantification by Echocardiography in Adults: An Update from the American Society of Echocardiography and the European Association of Cardiovascular Imaging. Eur Heart J Cardiovasc Imaging 2015;16:233-70. [Crossref] [PubMed]
- Echocardiography group of Chinese medical association. Guidelines for Performing Echocardiographic Examination in Adults. Chin J Ultrasonogr 2016;25:645-66.
- Mitchell C, Rahko PS, Blauwet LA, et al. Guidelines for Performing a Comprehensive Transthoracic Echocardiographic Examination in Adults: Recommendations from the American Society of Echocardiography. J Am Soc Echocardiogr 2019;32:1-64. [Crossref] [PubMed]
- Rietzschel ER, De Buyzere ML, Bekaert S, et al. Rationale, design, methods and baseline characteristics of the Asklepios Study. Eur J Cardiovasc Prev Rehabil 2007;14:179-91. [Crossref] [PubMed]
- Kuznetsova T, Herbots L, Lopez B, et al. Prevalence of left ventricular diastolic dysfunction in a general population. Circ Heart Fail 2009;2:105-12. [Crossref] [PubMed]
- Lancellotti P, Badano LP, Lang RM, et al. Normal Reference Ranges for Echocardiography: rationale, study design, and methodology (NORRE Study). Eur Heart J Cardiovasc Imaging 2013;14:303-8. [Crossref] [PubMed]
- Kou S, Caballero L, Dulgheru R, et al. Echocardiographic reference ranges for normal cardiac chamber size: results from the NORRE study. Eur Heart J Cardiovasc Imaging 2014;15:680-90. [Crossref] [PubMed]
- Gutgesell HP, Rembold CM. Growth of the human heart relative to body surface area. Am J Cardiol 1990;65:662-8. [Crossref] [PubMed]
- Anner J. Fallacy of per-weight and per-surface area standards, and their relation to spurious correlation. J Appl Physiol 1949;2:1-15. [Crossref] [PubMed]
- Lauer MS, Larson MG, Levy D. Gender-specific reference M-mode values in adults: population-derived values with consideration of the impact of height. J Am Coll Cardiol 1995;26:1039-46. [Crossref] [PubMed]
- Mawad W, Drolet C, Dahdah N, et al. A review and critique of the statistical methods used to generate reference values in pediatric echocardiography. J Am Soc Echocardiogr 2013;26:29-37. [Crossref] [PubMed]
- Neilan T G, Pradhan A D, Weyman A E. Derivation of a Size-Independent Variable for Scaling of Cardiac Dimensions in a Normal Adult Population. J Am Soc Echocardiogr 2008;21:779-85. [Crossref] [PubMed]
- Colan SD. The why and how of Z scores. J Am Soc Echocardiogr 2013;26:38-40. [Crossref] [PubMed]
- Haycock GB, Schwartz GJ, Wisotsky DH. Geometric method for measuring body surface area: a height-weight formula validated in infants, children, and adults. J Pediatr 1978;93:62-6. [Crossref] [PubMed]
- Cantinotti M, Scalese M, Murzi B, et al. Echocardiographic nomograms for chamber diameters and areas in Caucasian children. J Am Soc Echocardiogr 2014;27:1279-92. [Crossref] [PubMed]
- Cantinotti M, Scalese M, Murzi B, et al. Echocardiographic nomograms for ventricular, valvular and arterial dimensions in caucasian children with a special focus on neonates, infants and toddlers. J Am Soc Echocardiogr 2014;27:179-91. [Crossref] [PubMed]
- Kampmann C, Wiethoff CM, Wenzel A, et al. Normal values of M mode echocardiographic measurements of more than 2000 healthy infants and children in central Europe. Heart 2000;83:667-72. [Crossref] [PubMed]
- Koestenberger M, Nagel B, Ravekes W, et al. Reference values and calculation of z-scores of echocardiographic measurements of the normal pediatric right ventricle. Am J Cardiol 2014;114:1590-8. [Crossref] [PubMed]
- Pettersen MD, Du W, Skeens ME, et al. Regression equations for calculation of z scores of cardiac structures in a large cohort of healthy infants, children, and adolescents: an echocardiographic study. J Am Soc Echocardiogr 2008;21:922-34. [Crossref] [PubMed]
- Cantinotti M, Giordano R, Paterni M, et al. Adult echocardiographic nomograms: overview, critical review and creation of a software for automatic, fast and easy calculation of normal values. J Thorac Dis 2017;9:5404-22. [Crossref] [PubMed]
- Gokhroo RK, Anantharaj A, Bisht D, et al. A pediatric echocardiographic Z-score nomogram for a developing country: Indian pediatric echocardiography study - The Z-score. Ann Pediatr Cardiol 2017;10:31-8. [Crossref] [PubMed]
- Wang SS, Zhang YQ, Chen SB, et al. Regression equations for calculation of z scores for echocardiographic measurements of right heart structures in healthy Han Chinese children. J Clin Ultrasound 2017;45:293-303. [Crossref] [PubMed]
- Cantinotti M, Scalese M, Giordano R, et al. Three-Dimensional Echocardiography Derived Nomograms for Left Ventricular Volumes in Healthy Caucasian Italian Children. J Am Soc Echocardiogr 2019;32:794-97. [Crossref] [PubMed]
- Voges I, Giordano R, Koestenberg M, et al. Nomograms for Cardiovascular Magnetic Resonance Measurements in the Pediatric Age Group: To Define the Normal and the Expected Abnormal Values in Corrected/Palliated Congenital Heart Disease: A Systematic Review. J Magn Reson Imaging 2019;49:1222-35. [Crossref] [PubMed]
- Cantinotti M, Scalese M, Giordano R, et al. Normative Data for Left and Right Ventricular Systolic Strain in Healthy Caucasian Italian Children by Two-Dimensional Speckle-Tracking Echocardiography. J Am Soc Echocardiogr 2018;31:712-20. [Crossref] [PubMed]
- Pinto YM, Elliott PM, Arbustini E, et al. Proposal for a revised definition of dilated cardiomyopathy, hypokinetic non-dilated cardiomyopathy, and its implications for clinical practice: a position statement of the ESC working group on myocardial and pericardial diseases. Eur Heart J 2016;37:1850-8. [Crossref] [PubMed]
- Sluysmans T, Colan SD. Structural Measurements and Adjustments for Growth. In: Lai WW, Mertens LL, Cohen MS, et al. editors. Echocardiography in Pediatric and Congenital Heart Disease: From Fetus to Adult. Wiley-Blackwell, 2016.
- Pfaffenberger S, Bartko P, Graf A, et al. Size matters! Impact of age, sex, height, and weight on the normal heart size. Circ Cardiovasc Imaging 2013;6:1073-9. [Crossref] [PubMed]
- Packard GC, Boardman TJ. Model selection and logarithmic transformation in allometric analysis. Physiol Biochem Zool 2008;81:496-507. [Crossref] [PubMed]
- Mawad W, Drolet C, Dahdah N, et al. A Review and Critique of the Statistical Methods Used to Generate Reference Values in Pediatric Echocardiography. J Am Soc Echocardiogr 2013;26:29-37. [Crossref] [PubMed]
- Cline MG, Meredith KE, Boyer JT, et al. Decline of height with age in adults in a general population sample: estimating maximum height and distinguishing birth cohort effects from actual loss of stature with aging. Hum Biol 1989;61:415-25. [PubMed]


