Biomechanical finite element analysis of superior endplate collapse after thoracolumbar fracture surgery
Introduction
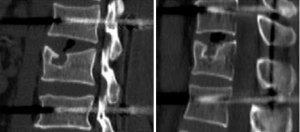
Vertebral fractures are common injuries in orthopedics. The thoracolumbar segment is the transition point between the mobile lumbar vertebrae and the fixed thoracic vertebrae and is also the site where stresses tend to be concentrated, accounting for approximately 28–60% of all spinal injury sites. Among the various types of internal fixation, posterior short-segment pedicle instrumentation (1,2) is the most common surgical approach in thoracolumbar fractures. However, complications such as “eggshell-like” changes, bone defects, and superior endplate collapse of the vertebral body can form after reduction (3-7). During the follow-up after internal fixation of thoracolumbar fractures, the imaging of some patients shows “crater-like” collapse of the superior endplate of the injured vertebra, with variable collapse area and depth, even involving the anterior edge of the vertebral body (Figure 1).
The innovation of this study is to introduce finite element analysis for the biomechanical study of the outcome of this type of collapse and to draw a practical conclusion on whether patients with this type of collapse on imaging are suitable for removal of the internal fixator. Our findings can be used as a reference for clinicians. It is hereby declared that this project does not involve medical ethics and does not require ethical review and approval.
Methods
Selection of experimental subject
The study was conducted in accordance with the Declaration of Helsinki and was approved by The Ethics Committee of Affiliated Hospital of Yangzhou University board of Xiaodan Liu, Kaizheng Gong, Jianhong Sun, Jiandong Tong, Kaidong Ji, Ming Jiang, Qiuping Luo, Shihua Li, Qing Ni, Anxiu Sun, Jianhong Sun, Peijian Zhang. Informed consent was taken from all the patients.
A healthy male volunteer, who was 27 years old with a height of 173 cm and a weight of 68 kg, was recruited. The subject gave informed consent to the experiment and signed a consent form. Through X-ray imaging examination, spinal skeletal deformity and injury as well as other lesions of the subject were excluded.
Instruments and software
Finite element analysis computer workstation
Lenovo ThinkStation P500; CPU: Xeon E5-1620v3; graphics card: Quadro K2200 4 GB; hard disk: 1 TB; memory: DDR4 RDIMM 128 GB; display: ViewSonic VX2370S-LED.
Three-dimensional modeling and finite element analysis software
Medical image processing software Mimics 15.0 (Materialise Company, Belgium); large computer-aided design software SolidWorks 2014 (SolidWorks Company, America); computer-aided engineering application software HyperMesh 12.0 (Altair Company, America); large finite element analysis software Abaqus 6.13 (Dassault Company, France).
Experimental methods
Sixty-four-slice spiral computed tomography (CT)
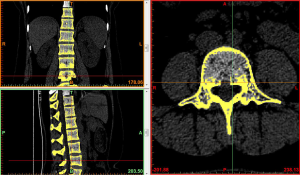
The volunteer took the supine position and underwent horizontal thin-section scanning from T11 to L3 to obtain 392 horizontal images of the corresponding segments. The scanning data were exported in DICOM format and were burned onto a CD for storage, so that the image data could be conveniently processed by the Mimics 15.0 medical image processing software.
Establishment of a three-dimensional finite element model of T11–L3
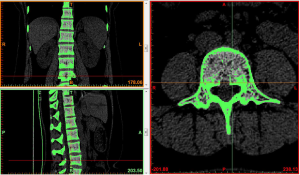
Image import: 392 horizontal images of the thoracolumbar spine in DICOM format were imported into Mimics 15.0 medical image processing software, which automatically located the images and displayed them according to the three orthogonal planes (coronal, horizontal, and sagittal), respectively (Figure 2).
Threshold segmentation: it was easy to distinguish the bones from the soft tissues based on the obvious differences in their CT values on the CT images by using the threshold segmentation method, and a mask was formed. If the gray values of adjacent pixels were close to each other and it was not easy to distinguish the boundary by the naked eye, the Draw Profile Line and the Thresholding functions in Mimics 15.0 medical image processing software were used to adjust the image threshold to 462–2,676 HU, so that the boundaries of the thoracolumbar vertebral body, intervertebral disc, sacrum, and facet joint were clearer (Figure 3).
Region growing and edit masks: the segmented regions on the above mask that were not connected to each other were formed into a new mask using region growing. The region growing feature was used to roughly extract various lumbar segments of interest. The boundary contour of each bone on each section of the scanned images was modified or erased to remove the unwanted hip bone portion, so that the boundary contour between bones could be accurately distinguished, especially the upper and lower facet joints (Figures 4,5).
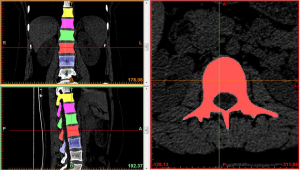
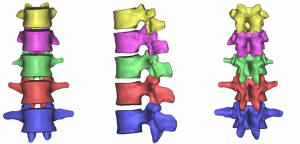
At the end of the tomographic image processing, three-dimensional surface model of the spine and pelvis was reconstructed using the three-dimensional calculation function of the software to generate independent skeletal models of each vertebral body and sacrum in order to clearly and directly reproduce the three-dimensional morphology of the bone structure. The image from the three-dimensional reconstruction could be demonstrated by rotation in all directions and translation. It was also possible to hide, delete, add, and merge the components as needed in this model to obtain different looks and effects (Figure 6).
The bone model reconstructed by the above method only contained three-dimensional surface elements with entities. The data of each bone model automatically included the position coordinates in the overall coordinate system of the vertebral body, and its information was exported through a point cloud and then imported into the reverse engineering software SolidWorks to further establish the entity model. SolidWorks preserved the original spatial relationship of each vertebral body without loss and directly formed the assembly.
The three-dimensional entity model of T11–L3 and the screw-rod system were constructed using SolidWorks (Figures 7-9).

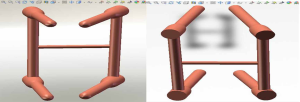
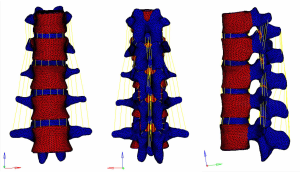
Meshing and supplemental establishment of the intervertebral disc and ligament: the three-dimensional entity models of T11–L3 and screw-rod system established in SolidWorks were imported into HyperMesh. Using the powerful mesh-making and dissection function of HyperMesh, a tetrahedral mesh was generated for the assembly, and 1-mm-thick cortical bone was constructed at the same time. The mesh sizes were 2 mm for T11–3 and 1 mm for the screw-rod system. Then, the structures of the endplate, annulus fibrosus, nucleus pulposus, anterior longitudinal ligament, posterior longitudinal ligament, intertransverse ligament, supraspinous ligament, interspinous ligament, ligamentum flavum, joint capsule ligament, and superior and inferior articular process cartilage were supplemented according to the anatomical site and shape to obtain a three-dimensional finite element model of T11–L3, which consisted of 191,386 elements and 55,741 nodes (the nodes and elements of T11–L3 Model Figure 10).
A three-dimensional finite element model of T11–L3 with the screw-rod system was obtained after the screw-rod system was added; it consisted of 310,970 elements and 73,469 nodes (the nodes and elements of T11–L3 Model with Pedicle Screw System Figure 11).

Models containing the implanted screw-rod system with five different defect sizes as well as five models with the screw-rod system removed were derived (defect diameters of 1/5, 2/5, 3/5, 4/5, and 5/5 of the anterior-two-thirds edge of the vertebral body, respectively) (Figure 12).
Assigning values to the model; using ABAQUS finite element analysis software for processing and analysis: in this experiment, another value assignment method in the finite element software was used, that is, the materials were assigned values taken from the parameters in past studies. The material properties of all tissues were considered homogeneous and isotropic (Table 1).
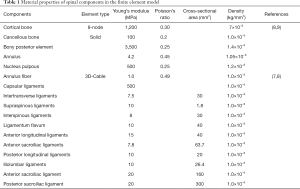
Full table
Note: for the parameters of this model, please refer to the table above, which are the same except those for the sacroiliac ligament, iliolumbar ligament, and density.
These ligaments were all simulated with Truss elements according to their function, and the properties of the Truss elements were defined such that there was no elastic force when compressed but there was elastic force when stretched; that is, the ligament elements only had tensile load. The number of Truss units was determined according to the cross-sectional area of the ligament, and in order to avoid concentrated local stress, the following settings were chosen: 20 anterior longitudinal ligaments, 20 posterior longitudinal ligaments, 16 interspinous ligaments, 12 supraspinous ligaments, 32 intertransverse ligaments, 20 ligamenta flavum, and 48 capsular ligaments, for a total of 168 Truss units. In the motion between lumbar facet joints, there were relative changes in position and friction, so we set this motion as an interaction, and the friction coefficient was defined as 0.2.
Validation of the model: there are many validation methods of finite element models, mainly including inspection, comparison with the same model in the past, and comparison with in vitro biomechanical experimental results. In this experiment, comparison with previous models was used to validate its effectiveness. (I) A vertical load of 1,200 N was applied to the complete model, and the axial compression stiffness was calculated. (II) A torque of 15 N·m was applied to the model, and the stiffness of the model under four working conditions (flexion, extension, lateral flexion, and rotation) was calculated. The compression and compression stiffness of the model were compared with those in the literature, and the results were similar (Table 2).

Full table
Results
The stress clouds for vertical load, forward flexion, posterior flexion, and lateral flexion of the normal vertebral body are shown in Figure 13.
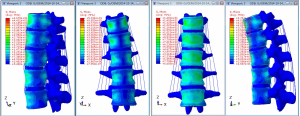
The images show that the anterior two-thirds of the vertebral body, the posterior part of the vertebral endplate, and the site near the pedicle were the areas with concentrated stress on the normal vertebral body in the vertical state, and the stress was distributed posteriorly and laterally. It was obvious that the stress on the cortical bone, especially the anterior edge of the vertebral body, was higher than that on the cancellous bone. When the vertebral body performed flexion or extension movement anteriorly, posteriorly, or laterally, concentrated stress occurred on both the flexion and extension sides and near the pedicle.
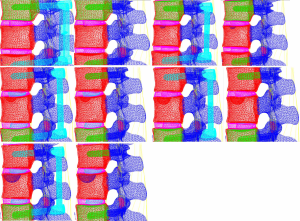
In the models with an implanted screw-rod system, the stress conditions of the five types of superior endplate collapse (defect volumes of 1/5, 2/5, 3/5, 4/5, and 5/5 of 2/3 of the anterior edge of the vertebral body, respectively) under vertical load, anteroposterior flexion, lateral flexion, and left-right rotation conditions were simulated. The stress distribution diagrams are shown in Table 3.
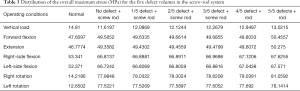
Full table
We analyzed the data as follows:
Group A (stress difference between the no-defect group and the 1/5 defect group);
Group B (stress difference between the 1/5 defect group and the 2/5 defect group);
Group C (stress difference between the 2/5 defect group and the 3/5 defect group);
Group D (stress difference between the 3/5 defect group and the 4/5 defect group);
Group E (stress difference between the 4/5 defect group and the 5/5 defect group).
Under each working condition, as the defect volume increased, the stress differences between consecutive groups were as listed in Table 4.
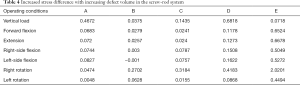
Full table
We used the data to generate a dot plot to more intuitively show the relationship between the defect volume and the increase in stress (Figure 14).
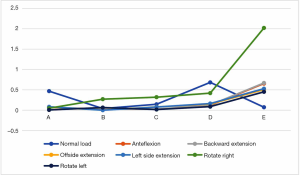
The 5/5 defect in the anterior column of the injured vertebra was a simulated extreme condition that does not exist in actual clinical practice, so we removed this condition from consideration. According to the chart, after the implantation of the internal fixator, the stress increased significantly when the injured vertebra showed a defect. As the defect volume increased, the stress increased correspondingly, and the increase in stress represented by group D (stress difference between the 3/5 defect group and the 4/5 defect group) was the greatest.
From the data analysis of the stress on the screw-rod system, it can be concluded that with the collapse of the superior endplate of the injured vertebra and the gradual increase in the defect volume of the anterior column, the stress gradually concentrated on the internal fixator (Table 5).
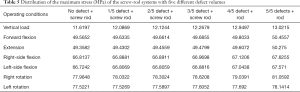
Full table
When the removal of the internal fixator was simulated, the stress outcomes of the five types of superior endplate collapse (defect volumes of 1/5, 2/5, 3/5, 4/5, and 5/5 of the anterior-two-thirds edge of the vertebral body, respectively) under vertical load, anteroposterior flexion, lateral flexion, and left and right rotation conditions. The stress distribution maps are shown in Table 6. We also made a table of the stress difference between the two groups in Table 7 and generated a dot plot (Figure 15). It can be seen that with the removal of the internal fixator and the loss of support from the internal fixator as well as the increase in defect volume, the stress gradually grew larger. The dot plot of the difference between groups showed that as the stress increased, the magnitude of change in the combined stress represented by group C (stress difference between the 2/5 defect group and the 3/5 defect group) under the seven working conditions was the largest, suggesting that after the removal of the internal fixator from injured vertebrae with superior endplate collapse and bone defect, when the collapse defect area reached 3/5 of the anterior column of the vertebral body, the concentration of stress increased significantly. This suggests that the risk of continued compression or even refracture of the injured vertebra increases after the removal of the internal fixator.
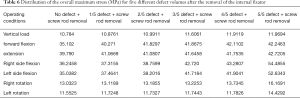
Full table
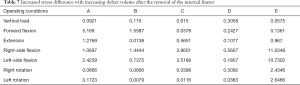
Full table
Discussion
As early as 1895, Kümmell first described the intravertebral vacuum sign in a study of postoperative kyphotic deformity, and later this feature was named Kümmell disease (10-13). Since then, many scholars at home and abroad have conducted extensive research on the pathogenesis of postoperative intravertebral vacuum sign and endplates, and the main theories on the mechanisms of postoperative collapse of injured vertebral bodies are as follows: (I) vertebral ischemic necrosis theory: Maldague et al. first linked the intravertebral vacuum sign to vertebral ischemic necrosis in 1978. This theory gained support from anatomical studies: the vasculature of the thoracolumbar spine is composed of pairs of segmental arteries, and the posterior central segmental branch behind the vertebral body supplies two adjacent vertebral bodies, while the anterior central branch on the ventral side of the vertebral body supplies one vertebral body. Therefore, theoretically, the ventral part of the vertebral body is at risk of insufficient blood supply, and this weak blood supply has been confirmed by Ratcliffe (14). (II) Formation of nonunion and pseudoarthrosis: although internal fixation supports and reduces the injured vertebra, the bony structures such as the internal trabecular bones are not recovered at the same time, leading to so-called eggshell vertebra. If activity persists and the fracture does not heal, then nonunion and pseudoarthrosis formation ensue (8). (III) When the patient takes the supine position, the traction effect between the intervertebral disc and ligament can partially restore the height of the vertebral body. Because the pressure in the vertebral body is lower than the external atmospheric pressure, Matzaroglou et al. (15) believed that a ruptured endplate, intervertebral disc, and vertebral fracture fissures with large gaps allowed air to enter easily, and when the vertebral body showed vacuum, it was often accompanied by the vacuum phenomenon of the intervertebral disc. (IV) Osteoporosis and the use of steroid drugs are considered the two most important risk factors leading to the vacuum phenomenon in the vertebral body (16). The higher the age of the patient and the lower the BMD, the higher the incidence of intravertebral cavity. Internal fixation by pedicle screws is a good method to treat thoracolumbar fracture. Specific operation process is not complex. First, we locate the injured vertebra by using “C” arm X-ray machine. Then insert the pedicle screws to superior vertebral body and inferior vertebral body. After distraction of injured vertebra, lock the screws at last. The C-arm fluoroscopy can accurately define position and monitor operation during the process as well as prevent complications. In addition to the above reasons, the self-deficiency of posterior pedicle internal fixation is also an important cause of vertebral empty shell degeneration and endplate collapse: (I) the long-term bone graft fusion rate of posterior surgery is lower than that of anterior surgery, and the bony structures such as the internal trabecular bones of the injured vertebra do not recover at the same time after internal fixation surgery, which leads to an eggshell-like change in the vertebral body in a long run (17). (II) Spinal injury often makes the anterior and middle columns lose their structural integrity, which directly decreases their ability to withstand longitudinal compressive loads, whereas the posterior internal fixation system lacks effective support for the anterior column, resulting in abnormal internal fixation loading. Even a solid internal fixation system can fail and have broken screws and rods due to fatigue (18), which can cause the reduced vertebral body to collapse again under compression before it heals. (III) The splinting effect of anterior and posterior longitudinal ligaments can reduce the anterior and posterior walls of the vertebral body and the height of the compressed vertebral body, but it cannot reduce the central area of the endplate with compression subsidence, and the intervertebral disc can be trapped in the vertebral body again (19). Excessive distraction of the injured vertebra can also cause the injured intervertebral disc tissue to fall into the vertebral body through a larger fissure in the vertebral body, thus hindering the bony healing inside the vertebral body, which eventually leads to vertebral vacuum sign and the collapse of the vertebral endplate. Based on the above theory, these defects of posterior pedicle screw fixation itself lead to the appearance of postoperative superior vertebral endplate collapse. Therefore, strict preoperative evaluation should be performed to understand its indications, and the indications for posterior surgery should not be expanded blindly. Detailed planning is required before any operation.Individualized treatment should be carried out according to each case. Treatment of thoracolumbar fracture with pedicle screw system has a long history, complications are also obvious. There are several important factors such as the patient’s age, BMD and centrum comminution degree. From my point of view, transpedicular bone grafting combined with pedicle screw internal fixation in the treatment of thoracolumbar fractures surgery can effectively prevent vertebral collapse phenomenon.
The finite element method used in this study has been widely used in spine research and has its unique, irreplaceable advantages. By comparing finite element analysis and experimental research, many scholars at home and abroad have confirmed that the analysis results of the finite element model are reliable. Goel et al. (20) first used the geometric shapes of CT scans to reconstruct a three-dimensional finite element model of a complex lumbar segment. Breau et al. (21) reported a detailed method for modeling using CT scan data of the lumbar spine. Ayturk et al. (22) studied the sensitivity and effectiveness of parameter convergence of finite element models of the human spine. In addition, many reports have confirmed the reliability of three-dimensional finite element methods for biomechanical analysis of the spine (9,23,24). Recently, Biswas et al. (25) used the finite element method to study the optimal internal screw fixation method for lower lumbar vertebra and concluded that finite element analysis was the most effective computer-aided tool for simulating spinal pathological conditions. Kulduk et al. (26) performed a biomechanical comparison of the dynamic stabilizing effect of internal fixations on spinal range of motion and loading characteristics using finite element models. Thus, the finite element method indeed has incomparable advantages in the study of lumbar diseases and the biomechanics of internal fixation.
Acknowledgments
Funding: None.
Footnote
Data Sharing Statement: Available at http://dx.doi.org/10.21037/atm-20-4091
Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/atm-20-4091). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The subject gave informed consent to the experiment and signed a consent form. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by The Ethics Committee of Affiliated Hospital of Yangzhou University board of Xiaodan Liu, Kaizheng Gong, Jianhong Sun, Jiandong Tong, Kaidong Ji, Ming Jiang, Qiuping Luo, Shihua Li,Qing Ni, Anxiu Sun, Jianhong Sun, Peijian Zhang. Informed consent was taken from all the patients.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Lindsey RW, Dick W. The fixateur interne in the reduction and stabilization of thoracolumbar spine fractures in patients with neurologic deficit. Spine 1991;16:S140-5. [PubMed]
- Dick W, Kluger P, Magerl F. A new device for internal fixation of thoracolumbar and lumbar spine fractures: the ‘fixateur interne’. Paraplegia 1985;23:225-32. [PubMed]
- Quillo-Olvera J, Lin GX, Jo HJ, et al. Complications on minimally invasive oblique lumbar interbody fusion at L2–L5 levels: a review of the literature and surgical strategies. Ann Transl Med 2018;6:101. [PubMed]
- Gurwitz GS, Dawson JM, McNamara MJ. Biomechanical analysis of three surgical approaches for lumbar burst fractures using short-segment instrumentation. Spine 1993;18:977-82. [PubMed]
- McCormack T, Karaikovic E, Gaines RW. The load sharing classification of spine fractures. Spine 1994;19:1741-4. [PubMed]
- McLain RF, Sparling E, Benson DR. Early failure of short-segment pedicle instrumentation for thoracolumbar fractures. A preliminary report. J Bone Joint Surg 1993;75:162-7. [PubMed]
- Sasso RC, Cotler HB. Posterior Instrumentation and Fusion for Unstable Fractures and Fracture-Dislocations of the Thoracic and Lumbar Spine: A Comparative Study of Three Fixation Devices in 70 Patients. Spine 1993;18:450-60. [PubMed]
- Pappou IP, Papadopoulos EC, Swanson AN. Osteoporotic vertebral fractures and collapse with intravertebral vacuum sign (Kummel's disease). Orthopedics 2008;31:61-6. [PubMed]
- Park WM, Park YS, Kim K. Biomechanical comparison of instrumentation techniques in treatment of thoracolumbar burst fractures: a finite element analysis. J Orthop Sci 2009;14:443-9. [PubMed]
- Libicher M, Appelt A, Berger I, et al. The intravertebral vacuum phenomen as specific sign of osteonecrosis in vertebral compression fractures: results from a radiological and histological study. Eur Radiol 2007;17:2248-52. [PubMed]
- Resnick D, Niwayama G, Guerra J Jr. Spinal vacuum phenomena: anatomical study and review. Radiology 1981;139:341-8. [PubMed]
- Kümmel H. Ueber die traumatischen Erkrankungen der Wirbelsaüle. Dtsch Med Wochenschr 1895;21:180-1.
- Yang H, Pan J, Wang G. A Review of Osteoporotic Vertebral Fracture Nonunion Management. Spine 2014;39:B4-6. [PubMed]
- Ratcliffe JF. The arterial anatomy of the adult human lumbar vertebral body: a microarteriographic study. J Anat 1980;131:57-79. [PubMed]
- Matzaroglou C, Georgiou CS, Panagopoulos A, et al. Kummell's Disease: Clarifying the Mechanisms and Patients' Inclusion Criteria. Open Orthop J 2014;8:288-97. [PubMed]
- Stäbler A, Schneider P, Link TM, et al. Intravertebral vacuum phenomenon following fractures: CT study on frequency and etiology. J Comput Assist Tomogr 1999;23:976-80. [PubMed]
- Shen J, Zou TM, Miu Y, Factors critical for creeping substitution of intracorporeal grafting following thoracolumbar fractures. Chinese J Tissue Engineer Res 2013;(53):9113-8.
- Liu G. Screw-rod fixation system for lumbar fractures: A mechanical analysis. Chinese Journal of Tissue Engineering Research 2011;(43):8147-50.
- Ambati DV, Wright EK Jr, Lehman RA Jr. Bilateral pedicle screw fixation provides superior biomechanical stability in transforaminal lumbar interbody fusion: a finite element study. Spine J 2015;15:1812-22. [PubMed]
- Goel VK, Kim YE, Lim T. An analytical investigation of the mechanics of spinal instrumentation. Spine 1988;13:1003-11. [PubMed]
- Breau C, Shirazi-Adl A, De Guise J. Reconstruction of a human ligamentous lumbar spine using CT images—a three-dimensional finite element mesh generation. Ann Biomed Eng 1991;19:291-302. [PubMed]
- Ayturk UM, Puttlitz CM. Parametric convergence sensitivity and validation of a finite element model of the human lumbar spine. Comput Methods Biomech Biomed Engin 2011;14:695-705. [PubMed]
- Qiu TX, Tan KW, Lee VS. Investigation of thoracolumbar T12–L1 burst fracture mechanism using finite element method. Med Eng Phys 2006;28:656-64. [PubMed]
- Imai K, Ohnishi I, Bessho M. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine 2006;31:1789-94. [PubMed]
- Biswas J, Karmakar S, Majumder S. Optimization of Spinal Implant Screw for Lower Vertebra through Finite Element Studies. J Long Term Eff Med Implants 2014;24. [PubMed]
- Kulduk A, Altun NS, Senkoylu A. Biomechanical comparison of effects of the Dynesys and Coflex dynamic stabilization systems on range of motion and loading characteristics in the lumbar spine: a finite element study. Int J Med Robot 2015;11:400-5. [PubMed]