Prognostic models for spinal metastatic disease: evolution of methodologies, limitations, and future opportunities
Spinal metastatic disease is present in 70% of cancer patients at autopsy with historical estimations of metastatic epidural spinal cord compression (MESCC) occurring in 2.5–10% of cancer patients in the last years of life (1-3). As a reference, 14.1 million new cases of cancer were diagnosed in 2012 and 22 million new cases are predicted to be diagnosed in 2030 (4).
Improvements in cancer therapy have increased survival of patients with metastatic disease and, in turn, the rate of MESCC (5,6). Simultaneously, randomized controlled trials showing improved quality of life with surgery and radiotherapy versus radiotherapy alone for MESCC have increased enthusiasm for and rates of surgical intervention (7,8). Surgical intervention to address spinal instability or cord compression is often undertaken to reduce pain, address neurologic deficit, or stabilize the spine (5,9-11). However, determination of the appropriateness of surgery requires preoperative estimation of postoperative survival, as well as postoperative complications, ambulatory status, neurologic deficit, and patient-reported quality of life. This assessment can inform multidisciplinary management and shared decision making with patients and families to consider timing of surgery, degree of invasiveness, expected postoperative recovery and alternative options of radiotherapy, medical management, and palliative therapy.
Regrettably, survival prediction on the basis of clinician judgement alone has been shown to be inaccurate and unreliable (12-14). Given the critical decisions that hinge on accurate survival prediction in MESCC, numerous predictive models have been developed to complement clinician judgement (15-36). Some of these scoring systems include Tokuhashi [1990], Bauer [1995], modified Bauer, Tomita [2001], Katagiri [2005], Sioutos [2005], van der Linden [2005], Oswestry Spinal Risk Index [2013], Bollen [2014], revised Katagiri [2014], New England Spine Metastasis (NESMS) Score [2015], SORG Nomogram [2016], SORG Classic [2016], and SORG Machine Learning algorithms [2019]. This article will focus specifically on survival prediction models in MESCC, as these are the most mature. However, the recommendations provided here can be translated to additional outcomes of interest as highlighted above.
Fundamentally, the motivation for predictive models is grounded in approximating the true relationship (transformation) between data available in the present (input) and survival expected in the future (output) (Figure 1).

Input
The inputs of models for MESCC consist of the factors gathered from the physical exam, medical history, laboratory tests, imaging, and pathology. Comparison of the predictive factors included by selected models is shown in Table 1. Other scoring systems and predictive factors include:

Full table
- North [2005]: surgical intervention greater than two spinal segments, recurrent disease after radiotherapy of operative site, primary tumor histology, cervical tumor location;
- Rades [2013]: primary tumor histology, bone metastasis, visceral metastasis, time from diagnosis to MESCC, ambulatory status before radiotherapy, timing of motor deficits relative to radiotherapy
The most common factors included in the prognostic models are primary tumor histology, metastatic tumor burden (e.g., visceral or brain metastasis, number of vertebral metastases), and performance/functional status (15-19,23,26,36). Considering the models developed in the last decade, additional factors included are previous systemic therapy and laboratory data (albumin, white blood cell, hemoglobin, neutrophil to lymphocyte ratio). Furthermore, the use of primary tumor histology in the models has changed dramatically. For example, early scoring systems stratified patients on the basis of the primary tumor location alone (e.g., lung versus breast). However, more recent systems such as the revised Katagiri not only include primary tumor location but also reflect advances in cancer biology with molecular characterization of the primary tumor (hormone dependent versus hormone independent breast cancer and molecularly targeted non-small cell lung cancer versus other lung cancers).
Advancements in cancer biology and novel biologic therapies (immunotherapy, targeted therapy) for specific expression profiles in primary tumor histologies would suggest inclusion of these important factors for accurate survival prediction. Other scoring systems developed for MESCC patients undergoing radiotherapy are more sophisticated in this manner. For example, previous studies have developed separate histology and age-specific MESCC radiotherapy scoring systems for prostate cancer (n=436), elderly prostate cancer (n=243), breast cancer (n=510), elderly breast cancer (n=218), non-small cell lung cancer (n=356), elderly lung cancer (n=201), colorectal cancer (n=121), elderly colorectal cancer (n=57), renal cell carcinoma (n=69), elderly renal cell carcinoma patients (n=71), myeloma (n=216), elderly myeloma (n=116), head-and-neck cancer (n=58), elderly patients with unknown primary (n=104), melanoma (n=27), gastric cancer (n=29), elderly gastric cancer (n=20), pancreatic cancer (n=15), esophageal cancer (n=27), hepatocellular carcinoma (n=8), salivary gland patients (n=9), and gynecologic malignancy (n=22) (37-52).
Most of the points above highlight the variety of the input data available for modeling. Spine surgeons should also be aware of the other 4 V’s (variety, volume, velocity, veracity), used most commonly with reference to “big data”, but also important for predictive modeling in general. Variety refers to the diversity of data included as highlighted above. Volume refers to sufficient quantities of patients to allow for reliable modeling as described below. Velocity is the expected rate of new data collection and availability for model derivation, update, and refinement. Veracity, perhaps the most important, defines the reliability of the input data and is a necessary pre-requisite for the trustworthiness of all subsequent steps in the modeling process. As the adage goes “garbage in, garbage out”, meaning that inaccurate or unreliable data will result in similarly unreliable models and outputs. Retrospective versus prospective study design, single-center versus multi-center, single-surgeon versus multiple, and one geography versus multiple all inform veracity of the data.
For the next step in evolution of inputs to MESCC prognostication models, there is a need for large multi-center prospective studies with granular, histology-specific data. The granular data should consist of the laboratory and biochemical prognostic factors identified previously but should also include information such as genomics, unstructured DICOM imaging, and passive and actively collected patient-reported outcomes (digital phenotyping). By integrating diverse data streams for focused populations, advancements in both basic cancer biology and computational methods can be applied for the benefit of MESCC patients.
Transformation and assessment methodology
Over time, the methodologies used for modeling the relationship between the preoperative MESCC patient data and the expected survival have evolved as well. Nearly all MESCC risk scores have used techniques such as proportional hazards regression or multivariable logistic regression. However, recent MESCC scoring systems (SORG) have explored more flexible modeling strategies such as stochastic gradient boosting, decision trees, random forests, kernel-based algorithms (Bayes point machine, support vector machines), neural networks, and elastic-net penalized logistic regression (23,32,36). The choice of fixed versus flexible modeling strategies depends on the tradeoff between bias and variance (53). In the context of MESCC, bias can be defined as the residual error in estimating the predicted survival on the basis of the available inputs. Variance can be defined as the generalizability of the model performance from the development population to future patients or external, independent populations. In general, a model can achieve nearly zero bias by employing the most flexible modeling strategy to perfectly memorize the relationship between the available inputs and outputs (observed survival). However, even if the model is 100% accurate on the population of patients used to develop the model, this does not guarantee that the model will be similarly accurate on future patients or external independent populations. In general, the bias (error on development population) decreases as the flexibility increases but the variance (error on future patients and independent populations) increases as the flexibility increases (53).
The purpose of modeling the transformation function between the available inputs in MESCC patients and the observed survival outcome is to achieve a balance between these competing forces. On the one hand, strategies such as multivariable logistic regression require and assume pre-specified relationships between the inputs and outputs. On the other hand, more flexible techniques such as convolutional neural networks act as universal functional approximators without requiring these pre-specified relationships. Determination of the appropriateness of one strategy over the other continues to be debated. Spine surgeons should be aware of both options and understand the strengths and limitations of each approach.
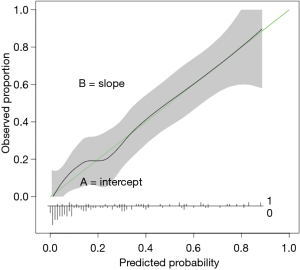
Steyerberg et al. previously described the (“ABCD”) principles that must be followed for validation of clinical prediction models (54). A and B refers to model calibration, C refers to model discrimination, and D refers to decision curve analysis (55). Calibration plots are constructed by plotting the models output (predicted) versus the observed events in the population of interest (Figure 2). “A” refers to calibration in the large and represents the intercept of the calibration plot. A perfect model would have calibration intercept =0. If the calibration intercept is greater than 0 and the predicted outcome is survival, the model tends to overestimate survival in the population relative to the observed outcome. The reverse occurs if the calibration intercept is less than zero. B refers to the calibration slope and represents the alignment of the predictor effects in the model relative to the observed outcome in the population. Perfect models have calibration slope =1.
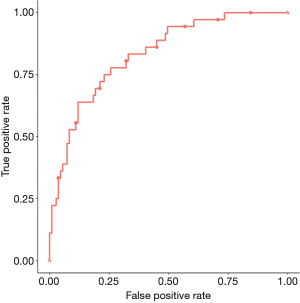
C refers to the model discrimination and represents the area under the receiver operating curve (AUC) (Figure 3). Perfect models have c-statistic or AUC =1. This metric conveys the probability that the model will be able to distinguish two patients from one another with respect to the outcome. This metric does not capture how the predictions align with the observed outcome. For example, consider that a model assigns a survival probability of 0.02 to every patient who dies at 90 days and assigns a probability of 0.03 to every patient who survives at 90 days. The c-statistic of the model will be perfect, but the calibration will be poor because we would expect that for 100 patients that the model predicts a survival probability of 0.03, only 3 of those 100 patients should be alive at 90 days. In fact, the reality will be very different, as reflected by the poor calibration.
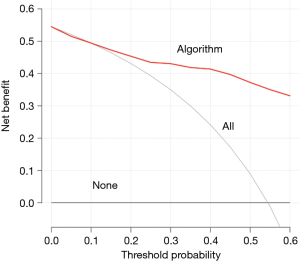
Finally, D refers to decision curve analysis, which is critical because neither discrimination nor calibration take into account the impact of true positives and false positives generated by these models (55). Decision curves are based on the idea of net benefit, which takes into account the impact of potential benefit and potential harm from the use of predictive models. Net benefit can be calculated for the model in the derivation or validation population by assessing the number of true positives, the number of false positives, the relative weight of true positives to false positives and finally the total number of patients in the population. The relative weight is calculated from the threshold probability, which is the probability above or below which the clinician will change management. For example, if the considered management change is a less invasive operation for MESCC, a potential threshold probability might be a predicted probability of survival less than 40% at 90 days. Curves are constructed for all threshold probabilities and the algorithm’s performance is compared to the default strategies for changing management for no patients or for all patients (Figure 4). In addition, decision curves are useful for comparing various scoring systems in order to identify the model that maximizes net benefit.
Ahmed et al. compared the SORG Classic, SORG nomogram, Tokuhashi, revised Tokuhashi, Tomita, Bauer, modified Bauer, Katagiri, and van der Linden scoring systems in 176 MESCC patients who underwent surgical resection at a single institution and found that the SORG nomogram had the highest AUC for 30-day (0.81) and 90-day (0.70) mortality (26). The original Tokuhashi score was best for 365-day survival (AUC =0.78) (26). A recent study comparing the Tokuhashi, revised Tokuhashi, Tomita, Bauer, van der Linden, Bartels, Oswestry Spinal Risk index, and Bollen scores in a prospective North American multi-center registry of 142 surgically treated MESCC patients found that the best c-statistic was Bartels (0.68) (56).
The same study was the first full validation of those models on both discrimination and calibration in accordance with the Transparent Reporting of Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD) guidelines (57). The best performing model on discrimination, Bartels, had a calibration slope of 0.45 and calibration plots of all scoring systems showed fair to poor calibration overall. Recent systems such as the SORG Machine Learning algorithms have included full assessment of the validation metrics advocated by Steyerberg et al. by assessing discrimination, calibration, and decision curve analysis. Future studies in MESCC that seek to develop or compare scoring systems should consider assessment of these important metrics, especially calibration and decision curve analysis as these represent the expected utility of these scoring systems in practice.
Output and model presentation
MESCC models can be presented as risk score tables, nomograms, and digital applications. Most of the available risk scores offer predictions in terms of an aggregate score that can be used against pre-specified categories defined in the derivation cohort. For example, application of the revised Tokuhashi score results in an aggregate score between 0 and 15. If patients have scores 0–8, they are predicted to survive less than 6 months, if they have scores 9–11, 6 months or more, if scores 12–15, 1 year or more. Drawbacks of risk scores are lack of predicted probabilities at specific time points critical for preoperative decision making. The SORG nomogram can be printed and used to compute a summary score based on the patient characteristics. This summary score is then scaled to probabilities of survival at specific time points (30 days, 90 days, 1 year). Alternatively, the SORG Machine Learning algorithms are available through an open-access web application for smartphones, tablets, or desktop computers and currently output probabilities and explanations for predicted survival at 90 days and 1 year after surgery (36).
Ideally, these scoring systems would be integrated into electronic health records. Such integration could allow the algorithms to automatically collect the relevant input data from the patient medical record. Subsequently, surgeons could access the outputs of these models when formulating the assessment and plan. The output would consist of both survival predictions and explanations for these predictions. With the model explanations, surgeons would have increased transparency into the factors used by the algorithms to make the predictions. Progress in machine learning methodologies allow for the use of flexible modeling strategies while maintaining the transparency required for clinicians to double-check the predictions of such algorithms against their own clinical expertise.
Final thoughts
Advances in basic biology and computational methodologies have created a host of opportunities for improving the care of MESCC patients; scoring systems represent an important subset of these opportunities. As highlighted in this article, spine surgeons should gain more familiarity with the evolution of existing scoring systems and the unique strengths and limitations in the pipeline of predictive analytics ranging from input to transformation to output. Future directions for the improvement of existing algorithms include several opportunities at each step in the model development pipeline; for example, inputs may be improved through the inclusion of more granular factors, such as tumor expression profiles, and assessment of emerging areas, such as unstructured data. Integration of algorithms into modern electronic health records may further facilitate the decision-making process in the future. Though clinician judgement alone may not be sufficient for prognostication in MESCC, clinician judgement is critical for maximizing the potential of more sophisticated and flexible modeling techniques. Previous studies have shown that patients benefit more from a combination of human (natural) intelligence and artificial intelligence rather than either alone (58). Finally, learnings from continued improvements in survival prediction models can subsequently be translated to developing models for complications, ambulatory status, neurologic deficit, and patient-reported outcomes.
Acknowledgments
None.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Lawton AJ, Lee KA, Cheville AL, et al. Assessment and Management of Patients With Metastatic Spinal Cord Compression: A Multidisciplinary Review. J Clin Oncol 2019;37:61-71. [Crossref] [PubMed]
- Loblaw DA, Laperriere NJ, Mackillop WJ. A population-based study of malignant spinal cord compression in Ontario. Clin Oncol (R Coll Radiol) 2003;15:211-7. [Crossref] [PubMed]
- Klimo P, Schmidt MH. Surgical management of spinal metastases. Oncologist 2004;9:188-96. [Crossref] [PubMed]
- Ferlay J, Soerjomataram I, Dikshit R, et al. Cancer incidence and mortality worldwide: sources, methods and major patterns in GLOBOCAN 2012. Int J Cancer 2015;136:E359-86. [Crossref] [PubMed]
- Verlaan JJ, Choi D, Versteeg A, et al. Characteristics of Patients Who Survived < 3 Months or > 2 Years After Surgery for Spinal Metastases: Can We Avoid Inappropriate Patient Selection? J Clin Oncol 2016;34:3054-61. [Crossref] [PubMed]
- Sciubba DM, Petteys RJ, Dekutoski MB, et al. Diagnosis and management of metastatic spine disease. A review. J Neurosurg Spine 2010;13:94-108. [Crossref] [PubMed]
- Kelly ML, Kshettry VR, Rosenbaum BP, et al. Effect of a randomized controlled trial on the surgical treatment of spinal metastasis, 2000 through 2010: a population-based cohort study. Cancer 2014;120:901-8. [Crossref] [PubMed]
- Patchell RA, Tibbs PA, Regine WF, et al. Direct decompressive surgical resection in the treatment of spinal cord compression caused by metastatic cancer: a randomised trial. Lancet 2005;366:643-8. [Crossref] [PubMed]
- Spiller W. Rapidly progressive paralysis associated with carcinoma. Arch Neurol Psychiatry 1925;13:471. [Crossref]
- Prasad D, Schiff D. Malignant spinal-cord compression. Lancet Oncol 2005;6:15-24. [Crossref] [PubMed]
- Barzilai O, Fisher CG, Bilsky MH. State of the Art Treatment of Spinal Metastatic Disease. Neurosurgery 2018;82:757-69. [Crossref] [PubMed]
- Chow E, Davis L, Panzarella T, et al. Accuracy of survival prediction by palliative radiation oncologists. Int J Radiat Oncol Biol Phys 2005;61:870-3. [Crossref] [PubMed]
- Chow E, Harth T, Hruby G, et al. How accurate are physicians' clinical predictions of survival and the available prognostic tools in estimating survival times in terminally ill cancer patients? A systematic review. Clin Oncol (R Coll Radiol) 2001;13:209-18. [PubMed]
- Parkes CM. Accuracy of predictions of survival in later stages of cancer. Br Med J 1972;2:29-31. [Crossref] [PubMed]
- Tomita K, Kawahara N, Kobayashi T, et al. Surgical strategy for spinal metastases. Spine 2001;26:298-306. [Crossref] [PubMed]
- Bauer HC, Wedin R. Survival after surgery for spinal and extremity metastases: prognostication in 241 patients. Acta Orthopaedica Scandinavica 1995;66:143-6. [Crossref] [PubMed]
- Tokuhashi Y, Matsuzaki H, Toriyama S, et al. Scoring system for the preoperative evaluation of metastatic spine tumor prognosis. Spine 1990;15:1110-3. [Crossref] [PubMed]
- Tokuhashi Y, Matsuzaki H, Oda H, et al. A revised scoring system for preoperative evaluation of metastatic spine tumor prognosis. Spine 2005;30:2186-91. [Crossref] [PubMed]
- van der Linden YM, Dijkstra SP, Vonk EJ, et al. Prediction of survival in patients with metastases in the spinal column: results based on a randomized trial of radiotherapy. Cancer 2005;103:320-8. [Crossref] [PubMed]
- Bollen L, van der Linden YM, Pondaag W, et al. Prognostic factors associated with survival in patients with symptomatic spinal bone metastases: a retrospective cohort study of 1 043 patients. Neuro Oncol 2014;16:991-8. [Crossref] [PubMed]
- Rades D, Hueppe M, Schild SE. A score to identify patients with metastatic spinal cord compression who may be candidates for best supportive care. Cancer 2013;119:897-903. [Crossref] [PubMed]
- Ghori AK, Leonard DA, Schoenfeld AJ, et al. Modeling 1-year survival after surgery on the metastatic spine. Spine J 2015;15:2345-50. [Crossref] [PubMed]
- Paulino Pereira NR, Janssen SJ, van Dijk E, et al. Development of a Prognostic Survival Algorithm for Patients with Metastatic Spine Disease. J Bone Joint Surg Am 2016;98:1767-76. [Crossref] [PubMed]
- Schoenfeld AJ, Le HV, Marjoua Y, et al. Assessing the utility of a clinical prediction score regarding 30-day morbidity and mortality following metastatic spinal surgery: the New England Spinal Metastasis Score (NESMS). Spine J 2016;16:482-90. [Crossref] [PubMed]
- Paulino Pereira NR, McLaughlin L, Janssen SJ, et al. The SORG nomogram accurately predicts 3- and 12-months survival for operable spine metastatic disease: External validation. J Surg Oncol 2017;115:1019-27. [Crossref] [PubMed]
- Ahmed AK, Goodwin CR, Heravi A, et al. Predicting survival for metastatic spine disease: a comparison of nine scoring systems. Spine J 2018;18:1804-14. [Crossref] [PubMed]
- Bartels RH, Feuth T, van der Maazen R, et al. Development of a model with which to predict the life expectancy of patients with spinal epidural metastasis. Cancer 2007;110:2042-9. [Crossref] [PubMed]
- Katagiri H, Takahashi M, Wakai K, et al. Prognostic factors and a scoring system for patients with skeletal metastasis. J Bone Joint Surg Br 2005;87:698-703. [Crossref] [PubMed]
- Katagiri H, Okada R, Takagi T, et al. New prognostic factors and scoring system for patients with skeletal metastasis. Cancer Med 2014;3:1359-67. [Crossref] [PubMed]
- Balain B, Jaiswal A, Trivedi JM, et al. The Oswestry Risk Index: an aid in the treatment of metastatic disease of the spine. Bone Joint J 2013;95-B:210-6. [Crossref] [PubMed]
- Sioutos PJ, Arbit E, Meshulam CF, et al. Spinal metastases from solid tumors. Analysis of factors affecting survival. Cancer 1995;76:1453-9. [Crossref] [PubMed]
- Karhade AV, Thio QCBS, Ogink PT, et al. Development of Machine Learning Algorithms for Prediction of 30-Day Mortality After Surgery for Spinal Metastasis. Neurosurgery 2018. [Epub ahead of print]. [Crossref] [PubMed]
- Fourney DR, Frangou EM, Ryken TC, et al. Spinal instability neoplastic score: an analysis of reliability and validity from the spine oncology study group. J Clin Oncol 2011;29:3072-7. [Crossref] [PubMed]
- North RB, LaRocca VR, Schwartz J, et al. Surgical management of spinal metastases: analysis of prognostic factors during a 10-year experience. J Neurosurg Spine 2005;2:564-73. [Crossref] [PubMed]
- Harrington KD. Metastatic disease of the spine. J Bone Joint Surg Am 1986;68:1110-5. [Crossref] [PubMed]
- Karhade AV, Thio QCBS, Ogink PT, et al. Predicting 90-Day and 1-Year Mortality in Spinal Metastatic Disease: Development and Internal Validation. Neurosurgery 2019. [Epub ahead of print]. [Crossref] [PubMed]
- Rades D, Fehlauer F, Schulte R, et al. Prognostic factors for local control and survival after radiotherapy of metastatic spinal cord compression. J Clin Oncol 2006;24:3388-93. [Crossref] [PubMed]
- Rades D, Douglas S, Veninga T, et al. A survival score for patients with metastatic spinal cord compression from prostate cancer. Strahlenther Onkol 2012;188:802-6. [Crossref] [PubMed]
- Rades D, Conde-Moreno AJ, Cacicedo J, et al. Metastatic Spinal Cord Compression: A Survival Score Particularly Developed for Elderly Prostate Cancer Patients. Anticancer Res 2015;35:6189-92. [PubMed]
- Douglas S, Huttenlocher S, Bajrovic A, et al. Prognostic factors for different outcomes in patients with metastatic spinal cord compression from cancer of unknown primary. BMC Cancer 2012;12:261. [Crossref] [PubMed]
- Rades D, Douglas S, Huttenlocher S, et al. Prognostic factors and a survival score for patients with metastatic spinal cord compression from colorectal cancer. Strahlenther Onkol 2012;188:1114-8. [Crossref] [PubMed]
- Rades D, Conde AJ, Garcia R, et al. A new instrument for estimation of survival in elderly patients irradiated for metastatic spinal cord compression from breast cancer. Radiat Oncol 2015;10:173. [Crossref] [PubMed]
- Rades D, Douglas S, Schild SE. A validated survival score for breast cancer patients with metastatic spinal cord compression. Strahlenther Onkol 2013;189:41-6. [Crossref] [PubMed]
- Rades D, Bartscht T, Janssen S, et al. Forecasting Survival Probabilities After Radiotherapy of Metastatic Epidural Spinal Cord Compression from Colorectal Cancer in the Elderly. Anticancer Res 2016;36:1829-33. [PubMed]
- Rades D, Douglas S, Veninga T, et al. A validated survival score for patients with metastatic spinal cord compression from non-small cell lung cancer. BMC Cancer 2012;12:302. [Crossref] [PubMed]
- Rades D, Bajrovic A, Bartscht T. Predictive Factors and a Survival Score for Patients Irradiated for Metastatic Spinal Cord Compression from Carcinoma of the Salivary Glands. Anticancer Res 2017;37:7011-5. [PubMed]
- Rades D, Dahlke M, Janssen S, et al. Radiation Therapy for Metastatic Spinal Cord Compression in Patients with Hepatocellular Carcinoma. In Vivo 2015;29:749-52. [PubMed]
- Rades D, Huttenlocher S, Bajrovic A, et al. A new instrument for estimating the survival of patients with metastatic epidural spinal cord compression from esophageal cancer. Radiol Oncol 2015;49:86-90. [Crossref] [PubMed]
- Rades D, Huttenlocher S, Bartscht T, et al. Predicting the survival probability of gastric cancer patients developing metastatic epidural spinal cord compression (MESCC). Gastric Cancer 2015;18:881-4. [Crossref] [PubMed]
- Huttenlocher S, Sehmisch L, Rudat V, et al. Motor function and survival following radiotherapy alone for metastatic epidural spinal cord compression in melanoma patients. J Dermatol 2014;41:1082-6. [Crossref] [PubMed]
- Rades D, Weber A, Bartscht T, et al. A new prognostic factor for the survival of patients with renal cell carcinoma developing metastatic spinal cord compression. Strahlenther Onkol 2014;190:667-70. [Crossref] [PubMed]
- Rades D, Douglas S, Veninga T, et al. Prognostic factors for local control and survival in patients with spinal cord compression from myeloma. Strahlenther Onkol 2012;188:628-31. [Crossref] [PubMed]
- Friedman J, Hastie T, Tibshirani R. The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Springer Series in Statistics). 2nd edition. New York: Springer, 2001.
- Steyerberg EW, Vergouwe Y. Towards better clinical prediction models: seven steps for development and an ABCD for validation. Eur Heart J 2014;35:1925-31. [Crossref] [PubMed]
- Vickers AJ, Elkin EB. Decision curve analysis: a novel method for evaluating prediction models. Med Decis Making 2006;26:565-74. [Crossref] [PubMed]
- Nater A, Tetreault LA, Kopjar B, et al. Predictive factors of survival in a surgical series of metastatic epidural spinal cord compression and complete external validation of 8 multivariate models of survival in a prospective North American multicenter study. Cancer 2018;124:3536-50. [Crossref] [PubMed]
- Collins GS, Reitsma JB, Altman DG, et al. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. BMC Medicine 2015;13:1. [Crossref] [PubMed]
- Senders JT, Arnaout O, Karhade AV, et al. Natural and Artificial Intelligence in Neurosurgery: A Systematic Review. Neurosurgery 2018;83:181-92. [Crossref] [PubMed]