The use of piecewise linear spline function on dose-response meta-analysis
Does-response meta-analysis is widely used in observational-based meta-analysis since proposed by Greenland et al. (1-4). The method works well in most of the situation, especially for the nonlinear trend approximating. Our argument is the linear slope insert within the function: by setting the parameters of quadratic and cubic term as zero. Linear relationship usually acts as main analysis when non-linear trend is non-significant or as additional analysis when non-linear trend is significant. Actually, only part of the linear slopes fit well (5). For J-shaped, U-shaped, S-shaped, and V-shaped curves, the linear slope fit bad since these slopes differ across pieces. We introduce a piecewise linear spline function that may be a solution for this issue (5,6). We assume log relative risks (LogRR) as dependent variable and exposure (X) as independent variable. Then a piecewise linear regression can be established as X against LogRR, with K indicates the cut points (knots) of the slopes.
If we take two knots as 30th, 60th of the distribution, which divide the function into three linear segments: 0th–30th; 30th–60th; 60th–100th.
In the Stata/SE 12.0 (Stata Corp., College Station, Texas, USA) software, mkspline procedure can be used to finish this work. Both one-step and two-step methods are available. Two-step method is recommended as it can reflect the heterogeneity across studies: first, estimating the coefficients of each segments of per unit increment of exposure within each study by mkspline procedure. Then summarizing the regression coefficients by random or fixed -effect model to produce a “mean” piecewise function.
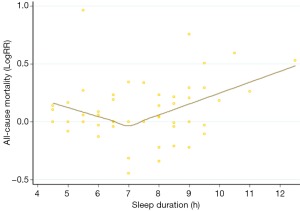
We take the meta-analysis as an example which investigates the relationship between sleep duration and risk of all-cause mortality (data can be obtained from the corresponding author) (6). It is worth to note that sleep duration trend to be U-shaped association to health problems (7,8).
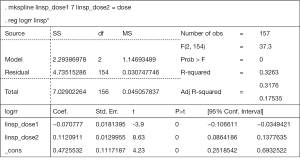
When fit with previous model (glst) by linear (1), we obtain the coefficient as 1.04 (95% CI: 1.02–1.06), which indicate that longer sleep duration is associated with higher risk of all-cause mortality; accordingly, the shorter one sleep, the lower risk he will be. This conclusion is obviously problematic. The correct way is to establish a piecewise linear slope (Figures S1-S3). With 1 knot (7 hours), we obtain two pieces of the slope: the coefficient at the left side of 7 hours is (−1.07; 95% CI: −1.03 to −1.11) and the coefficient of the right side of 7 hours is (1.12; 95% CI: 1.09–1.15), which suggest that, for those people who sleep less than 7 hours, shorter sleep duration is associated higher risk of all-cause mortality; while for people with more than 7 hours, longer sleep duration is also higher risk of all-cause mortality (6) (Figure S1).
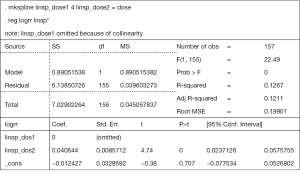
A simple method can be used to choose when to use linear model and piecewise one: the R2 comes with Mkspline. When we set the cut point on the lowest dose (or highest), then there is only one piece (between the lowest to the highest distribution) with the slope since the other one (from zero to the lowest or from the highest to highest) is defaulted to be omitted (Figure S2). By comparing the adjusted R2 between them we can get a more reasonable choice (9).
From the example, it is not hard to find that previous linear model may lead to incorrect conclusion. Actually, such incorrect use do occurred in published meta-analysis (10). In our opinion, the results of simple linear model should be treated with caution while piecewise linear model method should be widely considered in further dose-response meta-analysis.
Acknowledgements
None.
Stata code for piecewise model (one step method)
encode study, gen(studynum)
gen double logrr=log(adjrr)
gen double logub=log(ub)
gen double loglb=log(lb)
gen double se=(logub-loglb)/(2*invnormal(0.975))
mkspline linsp_dose1 7 linsp_dose2 = dose
reg logrr linsp*
lincom linsp_dose1*-1, eform
lincom linsp_dose2*1, eform
Stata code for simple linear model
encode study, gen(studynum)
gen double logrr=log(adjrr)
gen double logub=log(ub)
gen double loglb=log(lb)
gen double se=(logub-loglb)/(2*invnormal(0.975))
glst logrr dose, se(se) cov(n case) pfirst(id studynum) ts(r)
lincom dose*1, eform
Additional analysis
In our example, for the piecewise linear model, we got adjusted R2 as 0.32. The results of piecewise linear model with the cut point of 7 hours were showed below (Figure S1).
We can set the cut point as the lowest dose (4 hours) to test the adjusted R2 of simple linear model. As we can see that is omitted by the procedure and slope represents the slope of whole distribution (simple linear). The adjusted R2 is 0.12, therefore, it is more reasonable to use the piecewise linear model here (Figure S2). The results show a wild different with the glst procedure (1.02 vs. 1.04), may be due to the procedure itself and a random effect model the former used but current one does not.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Greenland S, Longnecker MP. Methods for trend estimation from summarized dose-response data, with applications to meta-analysis. Am J Epidemiol 1992;135:1301-9. [PubMed]
- Orsini N, Li R, Wolk A, et al. Meta-analysis for linear and nonlinear dose-response relations: examples, an evaluation of approximations, and software. Am J Epidemiol 2012;175:66-73. [Crossref] [PubMed]
- Rota M, Bellocco R, Scotti L, et al. Random-effects meta-regression models for studying nonlinear dose-response relationship, with an application to alcohol and esophageal squamous cell carcinoma. Stat Med 2010;29:2679-87. [Crossref] [PubMed]
- Crippa A, Discacciati A, Larsson SC, et al. Coffee consumption and mortality from all causes, cardiovascular disease, and cancer: a dose-response meta-analysis. Am J Epidemiol 2014;180:763-75. [Crossref] [PubMed]
- Yu YX, Zhang C, Weng H, et al. How to Conduct Dose-response Meta-analysis by Using Linear relation and Piecewise Linear Regression Model. Chinese Journal of Evidence-Based Medicine 2016;16:111-4.
- Liu TZ, Xu C, Rota M, et al. Sleep duration and risk of all-cause mortality: A flexible, non-linear, meta-regression of 40 prospective cohort studies. Sleep Med Rev 2016. [Epub ahead of print]. [Crossref] [PubMed]
- Cappuccio FP, D'Elia L, Strazzullo P, et al. Sleep duration and all-cause mortality: a systematic review and meta-analysis of prospective studies. Sleep 2010;33:585-92. [PubMed]
- Grandner MA, Schopfer EA, Sands-Lincoln M, et al. Relationship between sleep duration and body mass index depends on age. Obesity (Silver Spring) 2015;23:2491-8. [Crossref] [PubMed]
- Discacciati A, Crippa A, Orsini N. Goodness of fit tools for dose-response meta-analysis of binary outcomes. Res Synth Methods 2015. [Epub ahead of print]. [Crossref] [PubMed]
- Ruan H, Xun P, Cai W, et al. Habitual Sleep Duration and Risk of Childhood Obesity: Systematic Review and Dose-response Meta-analysis of Prospective Cohort Studies. Sci Rep 2015;5:16160. [Crossref] [PubMed]