Be care the risk of under fit in dose-response meta-analysis when using cubic spline

Dose-response meta-analysis (DMA) plays a vital role in investigating the potential causality between continuous variable and binary outcome. An increasing number of DMAs have been published during the past several years. In this letter, we aim to illustrate why some of them may at risk of under fit.

We searched Medline, Embase, and Wiley online Library for published DMAs between Jan-2011 to Dec-2015 and 427 publications were identified. We found that 187 DMAs used restricted cubic spline and 2 DMAs used natural cubic spline to fit the potential non-linear trend, with 143 (76.47%) of them used 3 knots (the minimum number). Our argument is that whether 3 knots is adequate representing the potential non-linear trend.

Stone (1) suggests using 5 knots for it flexibility enough representing the potential non-linear trend. While Durrleman (2) claims the number of knots may need to refer to the sample size that a reasonable large sample size can consider more knots and in most cases 3 knots is adequately. Such advisory opinions are valuable for us to select the number of knots. The most important one, however, such theories should be also correlated to clinical practice.

We took the recent published DMA (3) as an example (relevant data can be obtained by contacting the authors). The authors used restricted cubic spline with 5 knots (1^th, 25^th, 50^th, 75^th, and 99^th) to approximate the relationship between 24-hour sleep duration and risk of all-cause mortality and they found both shortened and prolonged sleep duration were associated with increased risk of all-cause mortality (J-shaped). We then re-analyzed their data by insetting 3 knots (1^th, 50^th, and 99^th) and found a totally different and unrealistic result: the shorter one sleep every day, the lower risk of all-cause mortality he will be (Figure 1A). This result is obviously ridiculous and will never possible in clinical practice. Similar but more close to reasonable result was found when using 4 knots (1^th, 25^th, 75^th, and 99^th), which indicated that 3 or 4 knots in such situation may at risk of under fit (Figure 1B).

Figure 1 The approximated non-linear trend between sleep duration and risk of all-cause mortality by using restricted cubic spline. (A) Using 3 knots; (B) using 4 knots. Relevant data and results of 5 knots can be obtained by connecting the authors of ref (3).

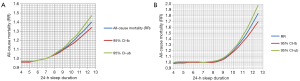
The authors of that DMA may also have found such phenomenon and made a correct response by using 5 knots. Their results and conclusions conform well to clinical practice which provides us a remarkable example.

Hypothetically, the results or conclusions of DMAs which only use 3 knots should be treated with caution since parts of them may be at risk of under fit. Therefore, when approximating non-linear relationship between exposure and outcome by cubic spline, we should take both theory and clinical practice into consideration. When conducting DMA by cubic spline with 3 knots in DMA, we recommend an additional analysis should be done by using 4, even 5 knots to verify whether 3 knots can fit the trend accurately and realistically. We also recommend that at least one clinician should be advised when preparing a systematic review or meta-analysis.

Acknowledgements

None.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Stone CJ. [Generalized Additive Models]: Comment. Statist Sci 1986;1:312-4. [Crossref]
2. Durrleman S, Simon R. Flexible regression models with cubic splines. Stat Med 1989;8:551-61. [Crossref] [PubMed]
3. Liu TZ, Xu C, Rota M, et al. Sleep duration and risk of all-cause mortality: A flexible, non-linear, meta-regression of 40 prospective cohort studies. Sleep Med Rev 2016. [Epub ahead of print]. [Crossref] [PubMed]